题目内容
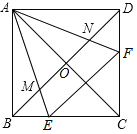
【题目】如图,点E,F分别为正方形ABCD的边BC,CD上一点,AC,BD交于点O,且∠EAF=45°,AE,AF分别交对角线BD于点M,N,则有以下结论:①∠AEB=∠AEF=∠ANM;②EF=BE+DF;③△AOM∽△ADF;④S△AEF=2S△AMN,以上结论中,正确的是______ .(请把正确结论的序号都填上)
【答案】①②③④
【解析】
如图,把△ADF绕点A顺时针旋转90°得到△ABH,由旋转的性质得,BH=DF,AH=AF,∠BAH=∠DAF,由已知条件得到∠EAH=∠EAF=45°,根据全等三角形的性质得到EH=EF,∴∠AEB=∠AEF,求得BE+BH=BE+DF=EF,故②正确;根据三角形的外角的性质得到∠ANM=∠AEB,于是得到∠AEB=∠AEF=∠ANM;故①正确;根据相似三角形的判定定理得到△OAM∽△DAF,故③正确;由△AMN∽△BME,得到![]() ,推出△AMB∽△NME,根据相似三角形的性质得到∠AEN=∠ABD=45°,推出△AEN是等腰直角三角形,根据勾股定理得到AE=
,推出△AMB∽△NME,根据相似三角形的性质得到∠AEN=∠ABD=45°,推出△AEN是等腰直角三角形,根据勾股定理得到AE=![]() AN,根据相似三角形的性质得到EF=
AN,根据相似三角形的性质得到EF=![]() MN,于是得到S△AEF=2S△AMN故④正确.
MN,于是得到S△AEF=2S△AMN故④正确.
如图,把△ADF绕点A顺时针旋转90°得到△ABH,
由旋转的性质得,BH=DF,AH=AF,∠BAH=∠DAF,
∵∠EAF=45°,
∴∠EAH=∠BAH+∠BAE=∠DAF+∠BAE=90°∠EAF=45°,
∴∠EAH=∠EAF=45°,
在△AEF和△AEH中,
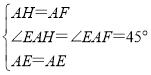 ,
,
∴△AEF≌△AEH(SAS),
∴EH=EF,
∴∠AEB=∠AEF,
∴BE+BH=BE+DF=EF,故②正确;
∵∠ANM=∠ADB+∠DAN=45°+∠DAN,
∠AEB=90°∠BAE=90°(∠HAB∠EAH)=90°(45°∠EAH)=45°+∠EAH,
∴∠ANM=∠AEB,
∴∠AEB=∠AEF=∠ANM;故①正确;
∵AC⊥BD,
∴∠AOM=∠ADF=90°,
∵∠MAO=45°∠NAO,∠DAF=45°∠NAO,
∴△OAM∽△DAF,故③正确;
连接NE,
∵∠MAN=∠MBE=45°,∠AMN=∠BME,
∴△AMN∽△BME,
∴![]() ,
,
∴![]() ,
,
∵∠AMB=∠EMN,
∴△AMB∽△NME,
∴∠AEN=∠ABD=45°,
∵∠EAN=45°,
∴∠NAE=∠NEA=45°,
∴△AEN是等腰直角三角形,
∴AE=![]() AN,
AN,
∵△AMN∽△BME,△AFE∽△BME,
∴△AMN∽△AFE,
∴![]() =
=![]() ,
,
∴EF=![]() MN,
MN,
∵AB=![]() AO,
AO,
∴S△AEF=S△AHE=![]() HEAB=
HEAB=![]() EFAB=
EFAB=![]()
![]() MN
MN![]() AO=2×
AO=2×![]() MNAO=2S△AMN.故④正确.
MNAO=2S△AMN.故④正确.
故答案为:①②③④.

 金状元绩优好卷系列答案
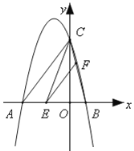
金状元绩优好卷系列答案【题目】已知二次函数y=ax2+bx+c中的y与x的部分对应值如下表:
x | ﹣1 | 0 | 1 | 3 |
y | ﹣3 | 1 | 3 | 1 |
下列结论中:①抛物线的开口向下;②其图象的对称轴为x=1;③当x<1时,函数值y随x的增大而增大;④方程ax2+bx+c=0有一个根大于4;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=3,其中正确的结论有( )
A.①②③B.①②③④⑤C.①③⑤D.①③④⑤