Question

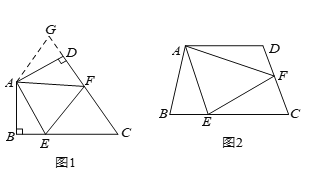
【题目】如图，张明同学想测量某铜像的高度，已知铜像（图中）高度比底座（图中）高度多1米，张明随后用高度为1米的测角仪（图中）测得铜像顶端点的仰角β＝51°24′，底座顶端点的仰角＝26°36′．请你帮助张明算出铜像AB的高度（把铜像和底座近似看在一条直线上它的抽象几何图形如左图）．（参考数据：sin26°36′≈0.45, cos26°36′≈0.89，tan26°36′≈0.5，sin51°24′≈0.78,cos51°24′≈0.6，tan51°24′≈1.25）

Answer 1

【答案】6米

【解析】分析: 首先设聂耳铜像AB的高度为xm，则可得BC=（x-2）m，然后分别在Rt△BCF中与在Rt△ACF中，利用正切函数的性质求得FC的值，即可得方程，解此方程即可求得答案.

详解: 设铜像的高度AB为x米，则BC=(x－2)米.

在Rt△BCF中，，

∴FC=.

在Rt△ACF中，

∵，

∴FC=.

∴2x－4=.

∴x=6.

答：铜像的高度AB为6米.