题目内容
【题目】如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.
(1)在图中画出与关于直线![]() 成轴对称的△A′B′C′;
成轴对称的△A′B′C′;
(2)线段CC′被直线![]() ;
;
(3)△ABC的面积为 ;
(4)在直线![]() 上找一点P,使PB+PC的长最短.
上找一点P,使PB+PC的长最短.

【答案】(1)图形见解析(2)垂直平分(3)3(4)图形见解析
【解析】试题分析:
(1)分别作出点C和点B关于l的对称点C’和B’,再顺次连接A’、B’、C’三点即可;
(2)由:轴对称的性质“连接对称点所得线段被对称轴垂直平分”可得结论;
(3)
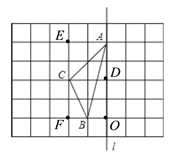
如图,可由“(△ACD的面积+梯形CBOD的面积)-△ABO的面积”来计算;也可由“矩形EFOA的面积-△AEC面积-△BCF的面积-△BOA的面积”来计算;
(4)连接CB’交l于点P,P为所求点;
试题解析:
(1)如图所示: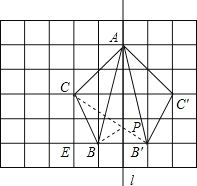
(2)∵△ABC与△AB′C′关于直线l成轴对称,
∴线段CC′被直线l垂直平分;
故答案为:垂直平分;
(3)如图(试题分析中):S△ABC=![]() ;
;
(4)连接B′C,交直线l与点P,此时PB+PC的长最短,

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目