题目内容
【题目】如图 1,CE 平分∠ACD,AE 平分∠BAC,且∠EAC+∠ACE=90°.
(1)请判断 AB 与 CD 的位置关系,并说明理由;
(2)如图 2,若∠E=90°且 AB 与 CD 的位置关系保持不变,当直角顶点 E 移动时,写出∠BAE 与∠ECD 的数量关系,并说明理由;
(3)如图 3,P 为线段 AC 上一定点,点 Q 为直线 CD 上一动点,且 AB 与 CD 的位置 关系保持不变,当点 Q 在射线 CD 上运动时(不与点 C 重合),∠PQD,∠APQ 与∠ BAC 有何数量关系?写出结论,并说明理由.

【答案】(1)![]() ,理由见解析;(2)
,理由见解析;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]() ,理由见解析.
,理由见解析.
【解析】
(1)根据角平分线的定义、平行线的判定即可得;
(2)根据平行线的性质(两直线平行,内错角相等)、三角形的外角性质即可得;
(3)根据平行线的性质(两直线平行,同旁内角互补)、三角形的外角性质、邻补角的定义即可得.
(1)![]() ,理由如下:
,理由如下:
![]() CE 平分
CE 平分![]() ,AE 平分
,AE 平分![]() ,
,![]()
![]()
![]()
![]() ;
;
(2)![]() ,理由如下:
,理由如下:
如图,延长AE交CD于点F,则![]()
![]()
![]()
由三角形的外角性质得:![]()
![]() ;
;
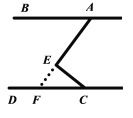
(3)![]() ,理由如下:
,理由如下:
![]()
![]() ,即
,即![]()
由三角形的外角性质得:![]()
又![]() ,即
,即![]()
![]()
即![]() .
.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目