题目内容
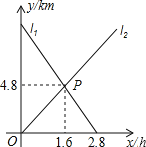
【题目】甲从A出发向B行走,同时乙从B出发向A行走,如图相交于点P的两条线段里l1、l2分别表示甲、乙距离B的路程y(km)与已用时间x(h)之间的关系.
(1)求甲乙行走的速度;
(2)求l1、l2的表达式;
(3)计算乙需多长时间到达A地.

【答案】(1)乙的速度为3(km/h);甲的速度为4(km/h);(2)l1=-4x+11.2,l2=3x;(3)乙需3.7小时到达A地.
【解析】
(1)乙的速度=行走的路程4.8km÷所用的时间1.6h;甲的速度=相遇后行走的路程4.8km÷相遇后用的时间1.2小时,把相关数值代入计算即可;
(2)利用待定系数法求一次函数解析式即可;
(3)利用(1)中所求,得出两地总路程,进而得出答案.
(1)乙的速度=4.8km÷1.6=3(km/h);
甲的速度=4.8km÷(2.8-1.6)=4(km/h).
(2)设l1=kx+b,将(1.6,4,8),(2.8,0)代入得出:![]() ,
,
解得:![]() ,
,
∴l1=-4x+11.2,
设l2=ax,将(1.6,4.8)代入得出:
4.8=1.6a,
解得:x=3,
∴l2=3x;
(3)由l1=-4x+11.2,当x=0时,l=11.2km,
11.2÷3=![]() (小时),
(小时),
答:乙需![]() 小时到达A地.
小时到达A地.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目







