��Ŀ����
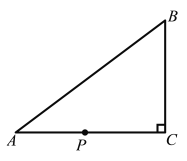
����Ŀ����ͼ����ABC�У���C=90��,AC=8cm,BC=6cm��������P�ӵ�C��ʼ����C��A��B��C��·���˶������ٶ�Ϊÿ��2cm�����˶���ʱ��Ϊt��.

��1����tΪ��ֵʱ��CP�ѡ�ABC���ܳ��ֳ���ȵ������֣�
��2����tΪ��ֵʱ��CP�ѡ�ABC������ֳ���ȵ������֣�
��3���ڣ�2��������£�������P��PE//BC������BC����һ��F��PE=CF������PF��
BE����̽��PF��BE��������ϵ.
���𰸡���1��t=6�룻��2��t=6.5�룻��3��������.
��������
��1�����ݹ��ɶ������AB���ɣ�
��2�����������ʽ�������з������ɣ�
��3������ȫ�������Σ�ͨ��ȫ�������ε��ж��������ʽ��н��.
�⣺

��1����ͼ1�� CP�ѡ�ABC���ܳ��ֳ���ȵ�������
�ߡ�C=90�㣬AC=8cm��BC=6cm
��![]()
�������AP=2t-8��BP=10-��2t-8��=10-2t+8=18-2t
��CP�ѡ�ABC���ܳ��ֳ���ȵ�������
��AC+AP=BC+BP����8+2t-8=6+18-2t�����t=6���룩��
��2����ͼ1����CP������ABC������ֳ���ȵ�������ʱ�������AB���ϣ�
��AP��BP�ֱ�Ϊ��APC����BPC�ĵױߣ����APC����BPC�й����ĸߣ�
�ߡ�APC����BPC�������ȣ�
��AP=BP=5��
��t=![]() =6.5���룩.
=6.5���룩.
��3����ͼ2������PC��
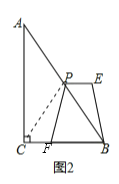
�ߵ�PΪֱ�ǡ�ABCб�ߵ��е㣬
��PC=PB����PCF=��PBC��
�֡�PE///BC��
���EPB=��PBC��
���EPB=��PCF��
�ڡ�PCF���BPE��
PC=PB ��PCF=��EPB CF=PE
���PCF�ա�BPE��SAS��
��PF=BE.

 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�