Ő‚ńŅńŕ»›
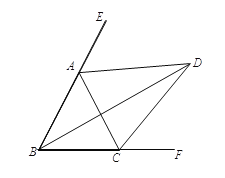
°ĺŐ‚ńŅ°Ņ»ÁÕľ1£¨‘ŕ![]() ÷–£¨
÷–£¨![]() ”ŕE£¨
”ŕE£¨![]() £¨D «AE…ŌĶń“ĽĶ„£¨«“
£¨D «AE…ŌĶń“ĽĶ„£¨«“![]() £¨Ń¨Ĺ”BD£¨CD£ģ
£¨Ń¨Ĺ”BD£¨CD£ģ

![]() ‘Ň–∂ŌBD”ŽACĶńőĽ÷√ĻōŌĶļÕ żŃŅĻōŌĶ£¨≤ĘňĶ√ųņŪ”…£Ľ
‘Ň–∂ŌBD”ŽACĶńőĽ÷√ĻōŌĶļÕ żŃŅĻōŌĶ£¨≤ĘňĶ√ųņŪ”…£Ľ
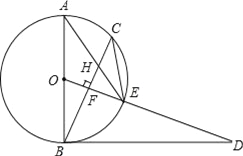
![]() »ÁÕľ2£¨»ŰĹę
»ÁÕľ2£¨»ŰĹę![]() »∆Ķ„E–ż◊™“Ľ∂®ĶńĹ«∂»ļů£¨ ‘Ň–∂ŌBD”ŽACĶńőĽ÷√ĻōŌĶļÕ żŃŅĻōŌĶ «∑Ů∑Ę…ķĪšĽĮ£¨≤ĘňĶ√ųņŪ”…£Ľ
»∆Ķ„E–ż◊™“Ľ∂®ĶńĹ«∂»ļů£¨ ‘Ň–∂ŌBD”ŽACĶńőĽ÷√ĻōŌĶļÕ żŃŅĻōŌĶ «∑Ů∑Ę…ķĪšĽĮ£¨≤ĘňĶ√ųņŪ”…£Ľ
![]() »ÁÕľ3£¨»ŰĹę
»ÁÕľ3£¨»ŰĹę![]() ÷–ĶńĶ»—Ł÷ĪĹ«»żĹ«–ő∂ľĽĽ≥…Ķ»ĪŖ»żĹ«–ő£¨∆šňŻŐűľĢ≤ĽĪš£ģ
÷–ĶńĶ»—Ł÷ĪĹ«»żĹ«–ő∂ľĽĽ≥…Ķ»ĪŖ»żĹ«–ő£¨∆šňŻŐűľĢ≤ĽĪš£ģ
![]() ‘≤¬ŌŽBD”ŽACĶń żŃŅĻōŌĶ£¨«Ž÷ĪĹ”–ī≥ŲĹŠ¬Ř£Ľ
‘≤¬ŌŽBD”ŽACĶń żŃŅĻōŌĶ£¨«Ž÷ĪĹ”–ī≥ŲĹŠ¬Ř£Ľ
![]() ń„ń‹«ů≥ŲBD”ŽACĶńľ–Ĺ«∂» ż¬ū£Ņ»ÁĻŻń‹£¨«Ž÷ĪĹ”–ī≥Ųľ–Ĺ«∂» ż£Ľ»ÁĻŻ≤Ľń‹£¨«ŽňĶ√ųņŪ”…£ģ
ń„ń‹«ů≥ŲBD”ŽACĶńľ–Ĺ«∂» ż¬ū£Ņ»ÁĻŻń‹£¨«Ž÷ĪĹ”–ī≥Ųľ–Ĺ«∂» ż£Ľ»ÁĻŻ≤Ľń‹£¨«ŽňĶ√ųņŪ”…£ģ
°ĺīūįł°Ņ(1)ľŻĹ‚őŲ;(2)ľŻĹ‚őŲ;(3) ĘŔBD=ACņŪ”…ľŻĹ‚őŲ;![]() ľŻĹ‚őŲ£ģ
ľŻĹ‚őŲ£ģ
°ĺĹ‚őŲ°Ņ
£®1£©Ņ…“‘÷§√ų°ųBDE°’°ųACEÕ∆≥ŲBD=AC£¨BD°ÕAC£ģ
£®2£©»ÁÕľ2÷–£¨≤Ľ∑Ę…ķĪšĽĮ£ģ÷Ľ“™÷§√ų°ųBED°’°ųAEC£¨Õ∆≥ŲBD=AC£¨°ŌBDE=°ŌACE£¨”…°ŌDEC=90°„£¨Õ∆≥Ų°ŌACE+°ŌEOC=90°„£¨“Úő™°ŌEOC=°ŌDOF£¨ňý“‘°ŌBDE+°ŌDOF=90°„£¨Ņ…Ķ√°ŌDFO=180°„£≠90°„=90°„£¨ľīŅ…÷§√ų£ģ
£®3£©ĘŔ»ÁÕľ3÷–£¨ĹŠ¬Ř£ļBD=AC£¨÷Ľ“™÷§√ų°ųBED°’°ųAECľīŅ…£ģ
Ęŕń‹£Ľ”…°ųBED°’°ųAECŅ…÷™£¨°ŌBDE=°ŌACE£¨Õ∆≥Ų°ŌDFC=180°„£≠£®°ŌBDE+°ŌEDC+°ŌDCF£©=180°„£≠£®°ŌACE+°ŌEDC+°ŌDCF£©=180°„£≠£®60°„+60°„£©=60°„ľīŅ…Ĺ‚ĺŲő Ő‚£ģ
Ĺ‚£ļ![]() £¨
£¨![]() £¨
£¨
ņŪ”… «£ļ—”≥§BDĹĽAC”ŕF£ģ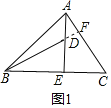
![]() £¨
£¨ ![]() £¨
£¨
‘ŕ![]() ļÕ
ļÕ![]() ÷–
÷–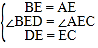
![]() °’
°’![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £Ľ
£Ľ![]() ≤Ľ∑Ę…ķĪšĽĮ£ģ
≤Ľ∑Ę…ķĪšĽĮ£ģ
»ÁÕľ2£¨ŃÓAC°ĘDEĹĽĶ„ő™O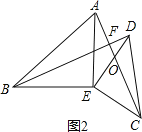
ņŪ”…£ļ![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
‘ŕ![]() ļÕ
ļÕ![]() ÷–
÷–
![]() °’
°’![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £Ľ
£Ľ
(3)![]() £Ľ
£Ľ
÷§√ų£ļ![]() ļÕ
ļÕ![]() «Ķ»ĪŖ»żĹ«–ő£¨
«Ķ»ĪŖ»żĹ«–ő£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
‘ŕ![]() ļÕ
ļÕ![]() ÷–
÷–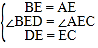
![]() °’
°’![]() £¨
£¨![]() £ģ
£ģ
Ęŕľ–Ĺ«ő™![]() £ģ
£ģ
Ĺ‚£ļ»ÁÕľ3£¨ŃÓAC°ĘBDĹĽĶ„ő™F£¨
”…ĘŔ÷™![]() °’
°’![]() £¨
£¨![]() £¨
£¨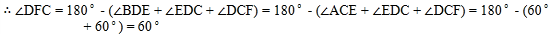 £¨ľīBD”ŽACňý≥…ĶńĹ«Ķń∂» żő™
£¨ľīBD”ŽACňý≥…ĶńĹ«Ķń∂» żő™![]() ĽÚ
ĽÚ![]()