题目内容
【题目】如图,已知Rt△ABC中,∠C=90°,∠A=60°,AC=3cm,AB=6m,点P在线段AC上以1cm/s的速度由点C向点A运动,同时,点Q在线段AB上以2cm/s的速度由点A向点B运动,设运动时间为t(s).
(1)当t=1时,判断△APQ的形状,并说明理由;
(2)当t为何值时,△APQ与△CQP全等?请写出证明过程.
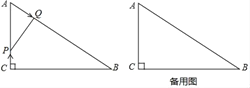
【答案】(1)△APQ是等边三角形;(2)t=1.5.
【解析】
(1)分别求出AP、AQ的长,根据等边三角形的判定定理即可得出结论;
(2)根据全等的条件和已知分别求出AP、CP、AQ、CQ的长,根据全等三角形的判定定理即可得出结论.
(1)△APQ是等边三角形.理由如下:
∵t=1,∴AP=3﹣1×1=2,AQ=2×1=2,∴AP=AQ.
∵∠A=60°,∴△APQ是等边三角形;
(2)存在t,使△APQ和△CPQ全等.当t=1.5s时,△APQ和△CPQ全等.理由如下:∵在Rt△ACB中,AB=6,AC=3,∴∠B=30°,∠A=60°,当t=1.5时,此时AP=PC.
∵t=1.5s,∴AP=CP=1.5cm.
∵AQ=3cm,∴AQ=AC.
又∵∠A=60°,∴△ACQ是等边三角形,∴AQ=CQ.
在△APQ和△CPQ中,∵AQ=CQ,AP=CP,PQ=PQ,∴△APQ≌△CPQ(SSS);
即存在时间t,使△APQ和△CPQ全等,时间t=1.5;

练习册系列答案
相关题目