题目内容
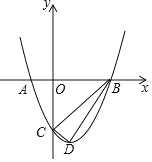
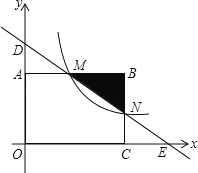
【题目】如图,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,B(4,2),过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
(1)直接写出直线DE的解析式_________;
(2)若反比例函数y=![]() (x>0)的图象与直线MN有且只有一个公共点,求m的值.
(x>0)的图象与直线MN有且只有一个公共点,求m的值.
(3)在分别过M,B的双曲线y=![]() (x>0)上是否分别存在点F,G使得B,M,F,G构成平行四边形,若存在则求出F点坐标, 若不存在则说明理由.
(x>0)上是否分别存在点F,G使得B,M,F,G构成平行四边形,若存在则求出F点坐标, 若不存在则说明理由.
【答案】(1)y=-![]() x+3;(2)4.5(3)(3,
x+3;(2)4.5(3)(3,![]() ).
).
【解析】
(1)将点D,E的坐标代入y=kx+b即可求出DE的解析式;
(2)联立直线MN解析式与反比例函数解析式,构造一元二次方程,使根的判别式为0即可;
(3)分别求出两条双曲线的解析式,设出点F,G的坐标,利用平行四边行的性质对边平行且相等及对角线互相平分,即可求出点F的坐标.
解:(1)设直线DE的解析式为y=kx+b,
将点D(0,3),E(6,0)代入y=kx+b中,
得![]()
解得,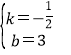
∴直线DE的解析式为y=-![]() x+3;
x+3;
(2) 由(1)知,直线DE的解析式为y=-![]() x+3,
x+3,
∴直线MN的解析式为y=-![]() x+3①,
x+3①,
∵反比例函数y=![]() (x>0)②,
(x>0)②,
联立①②化简得,x2-6x+2m=0,
∵反比例函数y=![]() (x>0)的图象与直线MN有且只有一个公共点,
(x>0)的图象与直线MN有且只有一个公共点,
∴△=36-4×2m=4(9-2m)=0,∴m=![]() ;
;
(3) )∵四边形OABC是矩形,
∴AB∥OC,AB=OC,
∵B(4,2),
∴点M的纵坐标为2,N的横坐标为4,
∵点M,N在直线DE:y=-![]() x+3上,当y=2时,-
x+3上,当y=2时,-![]() x+3=2,
x+3=2,
∴x=2,
∴M(2,2),
当x=4时,y=1,
∴N((4,1),
将M(2,2)代入y1=![]() ,
,
得,m=4,
∴y1=![]() ,
,
将B(4,2)代入y2=![]() ,
,
得,m=8,
∴y2=![]() ,
,
设G(a,![]() ),F(b,
),F(b,![]() ),
),
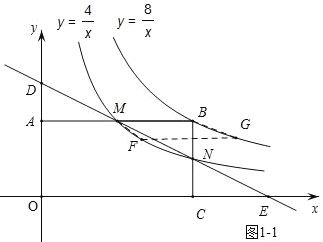
①假设存在,如图1-1,当MB作为平行四边形一边时,
∵MB=2,yM=yB,
∴GF=2,yF=yG,
∴ 或
或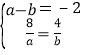
∴G(4,2),F(2,2),分别与B,M重合,舍去,
或G(-4,-2),F(-2,-2),在y轴左边,舍去;
②如图1-2,当MB为平行四边形对角线时,
MB与GF互相平分,
则![]() =
= ![]() =3,
=3,![]() =
= ![]() =2,
=2,
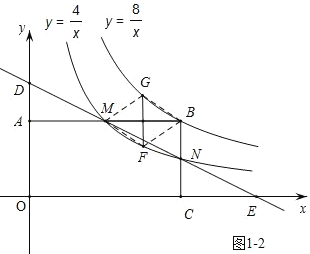
∴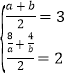
解得,![]() (舍去)或
(舍去)或![]()
∴G (3,![]() ),F(3,
),F(3,![]() ).
).
综上所述,点F坐标为(3,![]() ).
).

 小夫子全能检测系列答案
小夫子全能检测系列答案