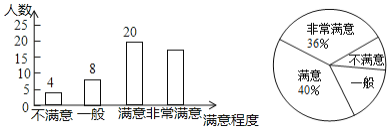
题目内容
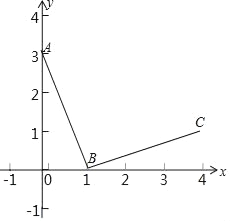
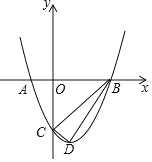
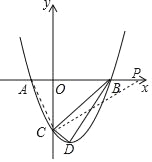
【题目】如图,O是坐标原点,过点A(﹣1,0)的抛物线y=x2﹣bx﹣3与x轴的另一个交点为B,与y轴交于点C,其顶点为D点.
(1)求b的值以及点D的坐标;
(2)连接BC、BD、CD,在x轴上是否存在点P,使得以A、C、P为顶点的三角形与△BCD相似?若存在,求出点P的坐标;若不存在,说明理由.
【答案】(1)b=2; D(1,﹣4).(2) 点P的坐标(0,0)(9,0).
【解析】
(1)根据待定系数法,可得函数解析式,根据配方法,可得顶点坐标;
(2)根据相似三角形的性质,可得AP的长,根据线段的和差,可得P点坐标.
解:(1)把A(﹣1,0)代入y=x2﹣bx﹣3,得1+b﹣3=0,
解得b=2.y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴D(1,﹣4).
(2)如图,当y=0时,x2﹣2x﹣3=0,
解得x1=﹣1,x2=3,即A(﹣1,0),B(3,0),D(1,﹣4).
由勾股定理,得BC2=18,CD2=1+1=2,BD2=22+16=20,BC2+CD2=BD2,∠BCD=90°,
①当△APC∽△DCB时,![]() ,即
,即![]() ,解得AP=1,即P(0,0).
,解得AP=1,即P(0,0).
②当△ACP∽△DCB时,![]() ,即
,即![]() ,解得AP=10,即P′(9,0).
,解得AP=10,即P′(9,0).
综上所述:点P的坐标(0,0)(9,0).

 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
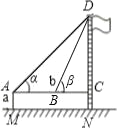
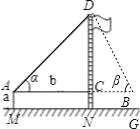
轻松课堂标准练系列答案【题目】某校九年级(2)班在测量校内旗杆高度的数学活动中,第一组的同学设计了两种测量方案,并根据测量结果填写了如下《数学活动报告》中的一部分.
课题 | 测量校内旗杆高度 | ||
目的 | 运用所学数学知识及数学方法解决实际问题﹣﹣﹣测量旗杆高度 | ||
方案 | 方案一 | 方案二 | 方案三 |
示意图 |
|
| |
测量工具 | 皮尺、测角仪 | 皮尺、测角仪 | |
测量数据 | AM=1.5m,AB=10m ∠α=30°,∠β=60° | AM=1.5m,AB=20m ∠α=30°,∠β=60° | |
计算过程(结 果保留根号) | 解: | 解: | |
(1)请你在方案一二中任选一种方案(多选不加分),根据方案提供的示意图及相关数据填写表中的计算过程、测量结果;
(2)请你根据所学的知识,再设计一种不同于方案一、二的测量方案三,并完成表格中方案三的所有栏目的填写.(要求:在示意图中标出所需的测量数据长度用字母a,b,c…表示,角度用字母α,β,γ…表示)