题目内容
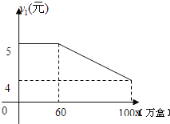
【题目】有一个茶叶厂,该厂的茶叶主要有两种销售方式,一种方式是卖给茶叶经销商,另一种方式是在各超市的柜台进行销售,每年该厂生产的茶叶都可以全部销售,该茶叶厂每年可以生产茶叶100万盒,其中,卖给茶叶经销商每盒茶叶的利润y1(元)与销售量x(万盒)之间的函数关系如图15所示;在各超市柜台销售的每盒利润y2(元)与销售量x(万盒)之间的函数关系为:当0≤x<40时, y2=—0.75x+80,
当40≤x≤100时 y2=40.
(1)写出该茶叶厂卖给茶叶经销商的销售总利润z1(万元)与其销售量x(万盒)之间的函数关系式,并指出x的取值范围;
(2)写出该茶叶厂在各超市柜台销售的总利润z2(万元)与卖给茶叶经销商的销售量x(万盒)之间的函数关系式及x取值范围;
(3)求该茶叶厂每年的总利润w(万元)与卖给茶叶经销商的销售量x(万盒)之间的函数关系式,并帮助该茶叶厂确定卖给茶叶经销商和在各超市柜台的销量各为多少万盒时,该公司的年利润最大.
【答案】(1)z1=![]() x+
x+![]() x(2)z2=40x+4000(3)该食品厂确定卖给各超市柜台的销量100万盒时,该公司的年利润最大
x(2)z2=40x+4000(3)该食品厂确定卖给各超市柜台的销量100万盒时,该公司的年利润最大
【解析】
(1)当0≤x<60时,可直接得出该茶叶厂卖给茶叶经销商的销售总利润z1=5,再根据当60≤x≤100时,每盒茶叶的利润y1(元)与销售量x(万盒)之间的函数图象过(60,5)(100,4)点,得出y1=-![]() x+
x+![]() ,最后乘以其销售量x即可得出答案;
,最后乘以其销售量x即可得出答案;
(2)根据在各超市柜台销售的每盒利润y2(元)与销售量x(万盒)之间的函数关系,用y2乘以卖给各超市柜台的销售量即可得出答案;
(3)分别求出当0≤x<40,40≤x<60,60≤x≤100时该茶叶厂每年的总利润w(万元)与卖给茶叶经销商的销售量x(万盒)之间的函数关系式为,再分别求出此时最大利润,即可得出所以该茶叶厂确定卖给各超市柜台的销量多少万盒时,该公司的年利润最大.
(1)当0≤x<60时,该食品厂卖给食品经销商的销售总利润z1=5,
∵当60≤x≤100时,每盒食品的利润y1(元)与销售量x(万盒)之间的函数图象过(60,5)(100,4)点,∴当60≤x≤100时,y1=![]() x+
x+![]() ,
,
∴当60≤x≤100时,该食品厂卖给食品经销商的销售总利润z1=(![]() x+
x+![]() )x
)x
=![]() x+
x+![]() x.
x.
(2)∵卖给食品经销商的销售量为x万盒,
∴在各超市柜台的销售量为(100x)万盒,,
∴当0≤100x<40,即60<x≤100时,该食品厂在各超市柜台销售的总利润z2(万元)与卖给食品经销商的销售量x(万盒)之间的函数关系式为:
z2=[0.75(100x)+80](100x)=0.75x2+70x+500,
当40≤100x≤100,即0≤x≤60时,该食品厂在各超市柜台销售的总利润z2(万元)与卖给食品经销商的销售量x(万盒)之间的函数关系式为:
z2=40(100x)=40x+4000,
(3)当60<x≤100时该食品厂每年的总利润w(万元)与卖给食品经销商的销售量x(万盒)之间的函数关系式为;
w=(![]() x+
x+![]() x)+(0.75x2+70x+500)
x)+(0.75x2+70x+500)
=![]() x+
x+![]() x+500,
x+500,
∵抛物线开口向下,∴x=1530/31时,w值最大,w=2387.82万元,
当40≤x<60时该食品厂每年的总利润w(万元)与卖给食品经销商的销售量x(万盒)间函数关系式为;
w=5x40x+4000=35x+4000,
∵该函数w随x的增大而减小,
∴当x=0时,利润最大,
此时的最大利润为:35×0+4000=4000(万元),
当0≤x<40时该食品厂每年的总利润w(万元)与卖给食品经销商的销售量x(万盒)之间的函数关系式为:
w=5x+(0.75x+80)(100x),
=0.75x2150x+8000,
∴当x=0时,利润最大,
此时的最大利润为8000(万元),
∴该食品厂确定卖给各超市柜台的销量100万盒时,该公司的年利润最大.

 口算题天天练系列答案
口算题天天练系列答案