题目内容
【题目】某商场以每件若千元的价格购进一批商品,当每件商品售价为360元时,每月可售出100件,每件获利20%. 为了扩大销售,商场决定采取适当降价的方式促销,经调查发现,如果每件商品降价5元,那么商场每月就可以多售出15件.
(1)该商品每件的进价是多少元?
(2)要使商场每月销售这种商品的利润达到6400元,且更有利于减少库存,则每件商品应降价多少元?
【答案】(1)300元(2)要使商场每月销售这种商品的利润达到6400元,且更有利于减少库存,则每件商品应降价20元
【解析】
(1)根据“成本×(1+利润率)=售价”列出方程即可求解;
(2)根据“每件利润×售出的件数=利润”列出方程,并根据实际意义取值即可得出答案.
解:(1)该商品每件的进价是a元,则,
a(1+20%)=360,
解得:x=300,
答:该商品每件的进价是300元;
(2)设每件商品应降价x元,由题意得,
(360﹣300﹣x)(![]() +100)=6400,
+100)=6400,
解得:x1=20,x2=![]() ,
,
∵有利于减少库存,且x取正整数,
∴x=20.
答:要使商场每月销售这种商品的利润达到6400元,且更有利于减少库存,则每件商品应降价20元.

【题目】某校九年级(2)班在测量校内旗杆高度的数学活动中,第一组的同学设计了两种测量方案,并根据测量结果填写了如下《数学活动报告》中的一部分.
课题 | 测量校内旗杆高度 | ||
目的 | 运用所学数学知识及数学方法解决实际问题﹣﹣﹣测量旗杆高度 | ||
方案 | 方案一 | 方案二 | 方案三 |
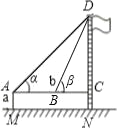
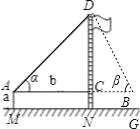
示意图 |
|
| |
测量工具 | 皮尺、测角仪 | 皮尺、测角仪 | |
测量数据 | AM=1.5m,AB=10m ∠α=30°,∠β=60° | AM=1.5m,AB=20m ∠α=30°,∠β=60° | |
计算过程(结 果保留根号) | 解: | 解: | |
(1)请你在方案一二中任选一种方案(多选不加分),根据方案提供的示意图及相关数据填写表中的计算过程、测量结果;
(2)请你根据所学的知识,再设计一种不同于方案一、二的测量方案三,并完成表格中方案三的所有栏目的填写.(要求:在示意图中标出所需的测量数据长度用字母a,b,c…表示,角度用字母α,β,γ…表示)