题目内容
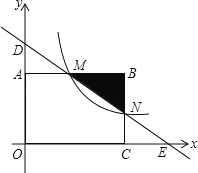
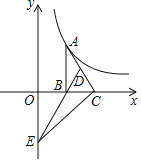
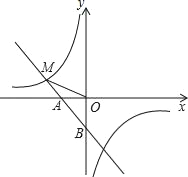
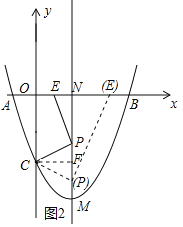
【题目】如图,抛物线y=x2-2x-3与x轴交于A,B两点,与y轴交于点C,其对称轴与抛物线相交于点M,与x轴相交于点N,点P是线段MN上的一个动点,连接CP,过点P作PE⊥CP交x轴于点E.
(1)求抛物线的顶点M的坐标;
(2)当点E与原点O的重合时,求点P的坐标;
(3)求动点E到抛物线对称轴的最大距离是多少?
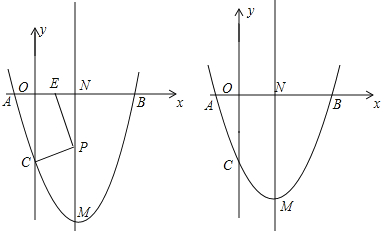
【答案】(1)(1,-4).(2)当点E与原点O的重合时,点P的坐标为(1,![]() )或(1,
)或(1,![]() ).(3)点E到抛物线对称轴的最大距离是4.
).(3)点E到抛物线对称轴的最大距离是4.
【解析】
(1)利用配方法将抛物线的解析式由一般式变形为顶点式,进而即可得出顶点M的坐标;
(2)利用二次函数图象上点的坐标特征可求出点C的坐标,过点C作CF⊥直线MN,垂足为点F,易证△PON∽△CPF,利用相似三角形的性质可得出关于PN长度的一元二次方程,解之即可得出PN的长,进而可得出点P的坐标;
(3)过点C作CF⊥直线MN,垂足为点F,设PN=m,分0<m<3,m=0或m=3,3<m≤4三种情况考虑:①当0<m<3时,由(2)可知:△PEN∽△CPF,利用相似三角形的性质可得出EN关于m的函数关系式,利用二次函数的性质即可解决最值问题;②当m=0或3时,点E和点N重合,此时EN=0;③当3<m≤4时,易证△PCF∽△EPN,利用相似三角形的性质可得出EN关于m的函数关系式,利用二次函数的性质即可解决最值问题.综上,取EN的最大值即可得出结论.
解:(1)∵y=x2-2x-3=(x-1)2-4,
∴抛物线的顶点M的坐标为(1,-4).
(2)当x=0时,y=x2-2x-3=-3,
∴点C的坐标为(0,-3).
过点C作CF⊥直线MN,垂足为点F,如图1所示.
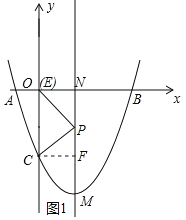
∵∠PON+∠OPN=90°,∠OPN+∠CPF=180°-∠CPO=90°,
∴∠PON=∠CPF.
又∵∠PNO=∠CFP=90°,
∴△PON∽△CPF,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴PN=![]() ,
,
∴当点E与原点O的重合时,点P的坐标为(1,![]() )或(1,
)或(1,![]() ).
).
(3)过点C作CF⊥直线MN,垂足为点F,设PN=m,分三种情况考虑,如图2所示.
①当0<m<3时,由(2)可知:△PEN∽△CPF,
∴![]() =
=![]() ,即
,即![]() =m,
=m,
∴EN=-m2+3m=-(m-![]() )2+
)2+![]() .
.
∵-1<0,
∴当m=![]() 时,EN取得最大值,最大值为
时,EN取得最大值,最大值为![]() ;
;
②当m=0或3时,点E和点N重合,此时EN=0;
③当3<m≤4时,∵∠PCF+∠CPF=90°,∠CPF+∠EPN=90°,
∴∠PCF=∠EPN.
又∵∠CFP=∠PNE=90°,
∴△PCF∽△EPN,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴EN=m2-3m.
∵1>0,
∴当3<m≤4时,EN的值随m值的增大而增大,
∴当m=4时,EN取得最大值,最大值为4.
综上所述:点E到抛物线对称轴的最大距离是4.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案【题目】水果基地为了选出适应市场需求的小西红柿秧苗,在条件基本相同的情况下,把两个品种的小西红柿秧苗各 300 株分别种植在甲、乙两个大棚. 对于市场最为关注的产量和产量的稳定性,进行了抽样调查,从甲、乙两个大棚各收集了 24 株秧苗上的小西红柿的个数,并对数据进行整理、描述和分析。
下面给出了部分信息:(说明:45 个以下为产量不合格,45 个及以上为产量合格,其中 45~65 个为产量良好,65~85 个为产量优秀)
a.补全下面乙组数据的频数分布直方图(数据分成 6 组: 25≤x<35,35≤x<45,45≤x<55,55≤x<65,65≤x<75,75≤x<85):
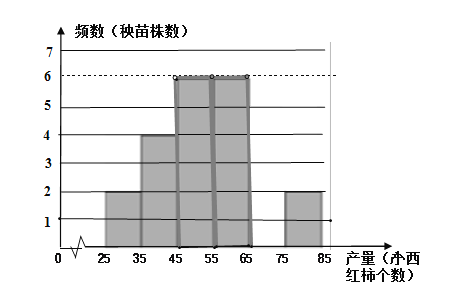
b.乙组数据在产量良好(45≤x<65)这两组的具体数据为: 46 46 47 47 48 48 55 57 57 57 58 61
c.数据的平均数、众数和方差如下表所示:
大棚 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 52.25 | 51 | 58 | 238 |
乙 | 52.25 | 57 | 210 |
(1)补全乙的频数分布直方图.
(2)写出表中![]() 的值.
的值.
(3)根据样本情况,估计乙大棚产量良好及以上的秧苗数为 株.
(4)根据抽样调查情况,可以推断出 大棚的小西红柿秧苗品种更适应市场需求,写出理由.(至少从两个不同的角度说明推断的合理性).