Question

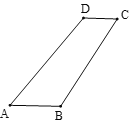
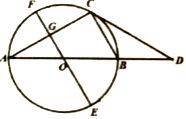
【题目】如图，⊙O是△ABC的外接圆，AB为⊙O的直径，过点C作∠BCD=∠CAB交AB的延长线于点D，过点O作直径EF∥BC，交AC于点G.

（1）求证：CD是⊙O的切线.

（2）若⊙O的半径为2，∠BCD=30°.

①连接AE、DE，求证：四边形ACDE是菱形.

②当点P是线段AD上的一动点时，求PF+PG的最小值.

Answer 1

【答案】（1）见解析；（2）①见解析，②PF+PG的最小值为.

【解析】

（1）连接OC，由AB是直径可得∠ACB=90°，由OC=OB可得∠ABC=∠OCB，由锐角互余的关系可得，即可得答案；（2）①连线AE、ED、BE，由∠BCD=30°，可得∠OCB=60°，进而可得∠OBC=60°，根据外角性质可得∠CDA=30°，即可证明∠CDA=∠CAD，可得AC=DC，由平行线性质可得，进而可得，即可证明ΔOCB，ΔOEB是等边三角形，易证明，，可得AC=CD=AE=ED即可得答案；②作F关于直线AB的对称点H，H在⊙O上，连接GH交AB于P点，此时线段GH最短，则PF+PG最小，连接OH，过H作HI⊥EF，可求出，，在Rt△AGO中，利用三角函数可求出OG的长，在Rt△HIO中可求出OI、HI的长，利用勾股定理求出GH的长即可.

（1）连接OC，

∵OC=OB，

∴，

∵AB是⊙O的直径，

∴，

∴，

∵，

∴，

∴OC⊥CD，

∴CD是⊙O切线.

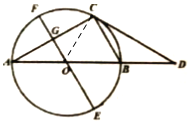
（2）①连线AE、ED、BE，

∵

∴

∴

∴AC=DC

∵EF∥BC

∴

∴

∵OE=OB=BE

∴ΔOCB，ΔOEB是等边三角形

∵BC=OB=BE

∴易证，

∴AC=CD=AE=ED

∴四边形ACDE是菱形，

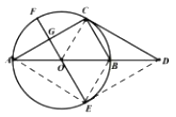
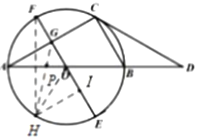
②作F关于直线AB的对称点H，H在⊙O上，连接GH交AB于P点，此时线段GH最短，则PF+PG最小，连接OH，过H作HI⊥EF

由①已证

又∵F于H关于直线AB对称

∴

∴，

在RtΔAGO中，OA=2

∴

在RtΔHIO中，OH=2

∴，

∴

∴PF+PG的最小值为