��Ŀ����
����Ŀ�����ڸ�����ͼ��G�͵�P������P��ͨ��һ�����ϻ�����ƽ��n��n��0������λ��ͼ��G��ij��P�䣬��Ƶ�PΪͼ��G�ġ��ɴ�㡱���ر�أ�����P��ͼ��G��ʱ����PΪͼ��G�ġ��ɴ�㡱��
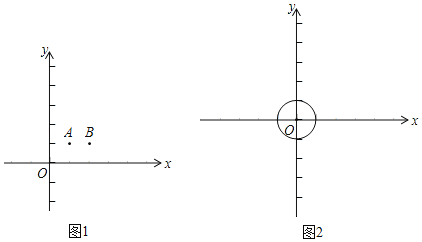
��1����ͼ1����ƽ��ֱ������ϵxOy�У���A��1��1����B��2��1����
���ڵ�O��A��B�У�����ֱ��y����x+2�ġ��ɴ�㡱������ ����
������A��ֱ��l�ġ��ɴ�㡱�ҵ�A����ֱ��l�ϣ�д��һ������Ҫ���ֱ��l�ı���ʽ���� ����
������A��B�����ҽ���һ����ֱ��y��kx+2�ġ��ɴ�㡱����k��ȡֵ��Χ���� ����
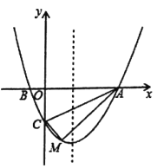
��2����ͼ2����ƽ��ֱ������ϵxOy�У���O�İ뾶Ϊ1��ֱ��l��y����![]() x+b��
x+b��
����b����2ʱ����ֱ��m��һ��N��xN��yN������N����O�ġ��ɴ�㡱��ֱ��д��xN��ȡֵ��Χ�� ����
����ֱ��m�����е���O�ġ��ɴ�㡱����һ�����Ȳ�Ϊ0���߶Σ�ֱ��д��b��ȡֵ��Χ�� ����
���𰸡���1����B����y����x+3������1��k����![]() ����2������3
����2������3![]() ��xN�ܩ�
��xN�ܩ�![]() ��1��xN��1������1��
��1��xN��1������1��![]() ��b��
��b��![]() ��
��
��������
��1���ٸ������ɴ�����Ķ��弴�ɽ�����⣮
�ڴ𰸲�Ψһ��ֱ���ڵ�A���Ϸ����ɣ�
�����ֱ��y��kx+2������A���Bʱk��ֵ�����жϣ�
��2���ٹ��㣨0��1���͵㣨0����1����x���ƽ���߷ֱ�ֱ��y����![]() x��2��N1����3
x��2��N1����3![]() ��1����N2����
��1����N2����![]() ����1�������㣨1��0���͵㣨��1��0����y���ƽ���߷ֱ�ֱ��y����
����1�������㣨1��0���͵㣨��1��0����y���ƽ���߷ֱ�ֱ��y����![]() x��2��N3��1����
x��2��N3��1����![]() ��2����N4����1��
��2����N4����1��![]() ��2�����ɴ˼����жϣ�
��2�����ɴ˼����жϣ�
�ڵ�N2��N3�غϣ�����Ϊ����1����1��ʱ����1��![]() +b���ɵ�b����1��
+b���ɵ�b����1��![]() ����ֱ��y��
����ֱ��y��![]() x+b���O����ʱ�����е�ΪE����y����F�������E�����꣬�����жϣ�
x+b���O����ʱ�����е�ΪE����y����F�������E�����꣬�����жϣ�
�⣺��1������ͼ1��1�У�
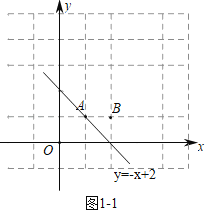
�����⣬��O����A��ֱ��y����x+2�����ɴ��������B����ֱ��y����x+2�����ɴ������
�ʴ�ΪB��
����ͼ1��2�У���A��ֱ��y����x+3�����ɴ�����ҵ�A����ֱ��l�ϣ��𰸲�Ψһ��ֱ���ڵ�A���Ϸ����ɣ���

�ʴ�Ϊy����x+3��
����ͼ1��3�У�

��ֱ��y��kx+2������Bʱ��k����![]() ��
��
��ֱ��y��kx+2������Aʱ��k����1��
�۲�ͼ���֪������A��B�����ҽ���һ����ֱ��y��kx+2�����ɴ������k��ȡֵ��Χ�ǩ�1��k����![]() ��
��
�ʴ�Ϊ��1��k����![]() ��
��
��2������ͼ2��1�У�

���㣨0��1���͵㣨0����1����x���ƽ���߷ֱ�ֱ��y����![]() x��2��N1����3
x��2��N1����3![]() ��1����N2����
��1����N2����![]() ����1����
����1����
���㣨1��0���͵㣨��1��0����y���ƽ���߷ֱ�ֱ��y����![]() x��2��N3��1����
x��2��N3��1����![]() ��2����N4����1��
��2����N4����1��![]() ��2����
��2����
�۲�ͼ���֪��N�ǡ�O�����ɴ������xN��ȡֵ��Χ��3![]() ��xN����
��xN����![]() ��1��xN��1��
��1��xN��1��
�ʴ�Ϊ��3![]() ��xN����
��xN����![]() ��1��xN��1��
��1��xN��1��
����ͼ2��2�У�

�ٵ�N2��N3�غϣ�����Ϊ����1����1��ʱ����1��![]() +b��
+b��
��b����1��![]() ��
��
�ڵ�ֱ��y��![]() x+b���O����ʱ�����е�ΪE����y����F��
x+b���O����ʱ�����е�ΪE����y����F��
��������Rt��OEF����OEF��90����OE��1����EOF��30����
OF��![]() ��
��![]() ��
��
�۲�ͼ���֪����������b��ֵΪ��1��![]() ��b��
��b��![]() ��
��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
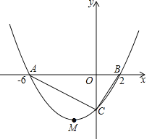
Сѧ��10����Ӧ����ϵ�д�����Ŀ����֪���κ���y��ax2+bx+c�У�����y���Ա���x�IJ��ֶ�Ӧֵ�����
x | �� | ��2 | ��1 | 0 | 1 | 2 | 3 | �� |
y | �� | ��8 | ��3 | 0 | 1 | 0 | ��3 | �� |
��A��m��y1����B��m��1��y2�����㶼�ڸú�����ͼ���ϣ���m���㷶Χ_____ʱ��y1��y2��