题目内容
【题目】已知抛物线![]() 和直线l:
和直线l:![]() .
.
(1)求证:抛物线与直线一定有两个不同的交点;
(2)设A、B是抛物线与直线的两个交点,点P是线段AB的中点,已知无论a为何值,点P在一条定抛物线上,试求这条定抛物线的解析式;
(3)设A、B是抛物线与直线的两个交点,将直线l向下平移7个单位恰好与抛物线有且只有一个公共点C,求△ABC的面积.
【答案】(1)详见解析;(2)y=4x2+5;(3)![]() .
.
【解析】
(1)由2x2=ax+5得2x2-ax-5=0,根据△=(-a)2-4×2×(-5)=a2+40>0即可得证;
(2)设点A(x1,ax1+5)、B(x2,ax2+5),由x1、x2为方程2x2-ax-5=0的两实数根知x1+x2=![]() ,根据点P为线段AB的中点知P(
,根据点P为线段AB的中点知P(![]() ),即可得点P的坐标为(
),即可得点P的坐标为(![]() +5),由4×(
+5),由4×(![]() +5知点P在抛物线y=4x2+5上;
+5知点P在抛物线y=4x2+5上;
(3)由平移后的直线y=ax-2与抛物线只有一个交点知ax-2=2x2有唯一解,据此求得a的值,即可得出点A、B、C的坐标,利用割补法求解可得答案.
(1)由2x2=ax+5得2x2-ax-5=0,
∵△=(-a)2-4×2×(-5)=a2+40>0,
∴抛物线与直线一定有两个不同的交点;
(2)设点A(x1,ax1+5)、B(x2,ax2+5),
则x1、x2为方程2x2-ax-5=0的两实数根,
∴x1+x2=![]() ,
,
∵点P为线段AB的中点,
∴点P(![]() ),即(
),即(![]() ),
),
∴点P的坐标为(![]() +5),
+5),
∵4×(![]() +5,
+5,
∴点P在抛物线y=4x2+5上;
(3)直线l:y=ax+5向下平移7个单位后的直线为y=ax-2,
根据题意知,ax-2=2x2,即2x2-ax+2=0有唯一解,
则(-a)2-4×2×2=0,
解得:a=4或a=-4,
当a=4时,方程为2x2-4x+2=0,解得x=1,
则点C坐标为(1,2),
此时直线l的解析式为y=4x+5,
由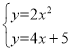 得
得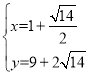 或
或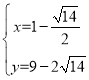 ,
,
即点A(1-![]() )、B(1+
)、B(1+![]() ),
),
如图1,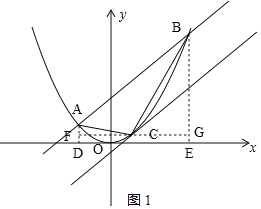
S△ABC=S梯形AFGB-S△ACF-S△BCG=![]() ;
;
当a=-4时,方程为2x2+4x+2=0,解得x=-1,
则点C坐标为(-1,2),
此时直线l的解析式为y=-4x+5,
由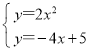 得
得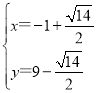 或
或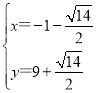 ,
,
即点A(-1-![]() ),
),
如图2,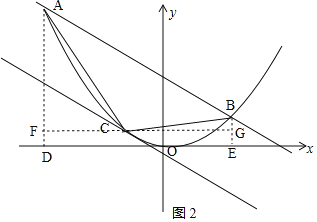
S△ABC=S梯形AFGB-S△ACF-S△BCG=![]() ;
;
综上,△ABC的面积为![]() .
.