Question

【题目】如图，在Rt△ABC中，∠C＝90°，点D在AB上，以AD为直径的⊙O与BC相交于点E，与AC相交于点F，AE平分∠BAC．

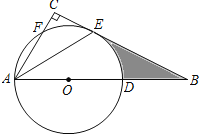
（1）求证：BC是⊙O的切线．

（2）若∠EAB＝30°，OD＝3，求图中阴影部分的面积．

（3）若AD＝5，AE＝4，求AF．

Answer 1

【答案】（1）详见解析；（2）；（3）

【解析】

（1）如图，连结OE，由角平分线的定义可得∠CAE＝∠EAD，由等腰三角形的性质可得∠EAD＝∠OEA，即可证明∠OEA＝∠CAE，可得OE//AC，根据平行线的性质可得∠OEB＝∠C＝90°，即可证明BC是⊙O的切线；（2）由角平分线的定义可得∠EOD＝60°，即可得出∠B=30°，根据含30°角的直角三角形的性质可求出OB的长，利用勾股定理求出BE的长，根据S阴影=S△OEB-S扇形OED即可得答案；（3）如图，连接DE，EF，由AD是直径可得∠AED=90°，利用勾股定理可求出DE的长，由∠CAE＝∠EAD，∠ACE＝∠AED＝90°可证明△ACE∽△AED，根据相似三角形的性质可求出AC、CE的长，∠ADE＝∠AEC，由圆内接四边形的性质可得∠CFE＝∠ADE，可得∠AEC＝∠CFE，即可证明△CEF∽△CAE，根据相似三角形的性质可求出CF的长，根据AF=AC-CF可得答案.

（1）如图，连接OE，

∵AE平分∠BAC，

∴∠CAE＝∠EAD，

∵OA＝OE，

∴∠EAD＝∠OEA，

∴∠OEA＝∠CAE，

∴OE∥AC，

∴∠OEB＝∠C＝90°，

∴OE⊥BC，

∴BC是⊙O的切线.

（2）解：∵∠EAB＝30°，AE平分∠BAC，

∴∠EOD＝60°，

∴∠OEB＝90°，

∴∠B＝30°，

∴OB＝2OE＝2OD＝6，

∴，

∴

，

∴．

（3）如图，连接DE，EF，

∵AD为⊙O的直径，

∴∠AED＝90°，

∴，

∵AE平分∠BAC，

∴∠CAE＝∠EAD，

又∵∠ACE＝∠AED＝90°，

∴△ACE∽△AED，

∴，∠ADE＝∠AEC，

∴，

∵四边形AFED为圆内接四边形，

∴∠AFE+∠ADE=180°，

∵∠CFE+∠AFE=180°，

∴∠CFE＝∠ADE，

∴∠AEC＝∠CFE，

∵∠FCE＝∠ACE，

∴△CEF∽△CAE，

∴，

∴，

∴AF＝AC﹣CF＝．