题目内容
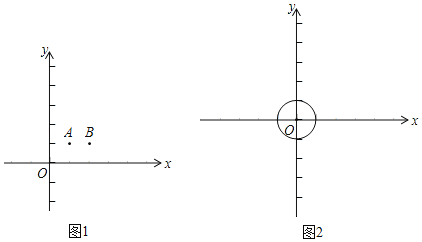
【题目】已知点A、B(AB<2),现没有直尺,只有一把生锈的圆规,仅能做出半径为1的圆,能否在平面内找到一点F,使得△ABF是等边三角形?
小天经过探究完成了以下的作图步骤:
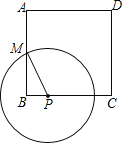
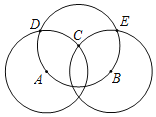
第一步:分别以点A、B为圆心,1为半径作圆,两圆交于点C;
第二步:以C为圆心,1为半径作圆交第一步中的两圆于点D、E;
第三步:分别以D、E为圆心,1为半径作圆,两圆交于点C、F,
(1)请将图补充完整,并作出△ABF.
(2)以下说法中,
①点C在线段AB的垂直平分线上;
②△CAD和△CBE都是等边三角形;
③点C在线段AF的垂直平分线上;
④△ABF是等边三角形,
正确的有 .(填上所有正确的序号)
【答案】(1)详见解析;(2)①②④.
【解析】
(1)按第三步作图,两圆交于点C,F,连结AF,BF,AB,得到△ABF是等边三角形;
(2)由作图步骤及圆的性质可对结论判断即可.
解:(1)如图,连结AF,BF,AB,则△ABF是等边三角形;
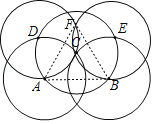
(2)∵分别以点A、B为圆心,1为半径作圆,两圆交于点C,
∴AC=BC,
∴点C在线段AB的垂直平分线上,
故①正确;
∵分别以点A、B为圆心,1为半径作圆,两圆交于点C;以C为圆心,1为半径作圆交第一步中的两圆于点D、E;
∴AD=AC=DC=1,BC=CE=BE=1,
∴△CAD和△CBE都是等边三角形,
故②正确,
由作图可知AC=1,而CF≠1,
∴点C不在线段AF的垂直平分线上,
故③错误;
由①知点C在线段AB的垂直平分线上,
∴点F在线段AB的垂直平分线上,
∴AF=BF,
同理AB=BF,
∴△ABF是等边三角形,
故④正确.
故答案为:①②④.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目