题目内容
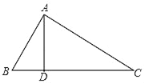
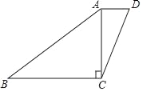
【题目】如图,一张四边形纸片ABCD,AB=20,BC=16,CD=13,AD=5,对角线AC⊥BC.
(1)求AC的长;
(2)求四边形纸片ABCD的面积;
(3)若将四边形纸片ABCD沿AC剪开,拼成一个与四边形纸片ABCD面积相等的三角形,直接写出拼得的三角形各边高的长.
【答案】(1)12;(2)126;(3)12;![]()
![]()
【解析】
(1)由勾股定理可直接求得结论;
(2)根据勾股定理逆定理证得∠CAD=90,由于四边形纸片ABCD的面积=S△ABC+S△ACD,根据三角形的面积公式即可求得结论;
(3)由于将四边形纸片ABCD沿AC剪开,得到△ABC和△ACD的相等的边是AC,拼成一个与四边形纸片ABCD面积相等的三角形,只有将AC重合,故可拼成如图所示的图形.
(1)在Rt△ABC中,AC![]() 12;
12;
(2)∵AD2+AC2=52+122=133=CD2,∴∠CAD=90°,∴四边形纸片ABCD的面积=S△ABC+S△ACD![]() ACBC
ACBC![]() ACAD
ACAD![]() 12×16
12×16![]() 12×5=126;
12×5=126;
(3)如图,∵AB=20,BC=16,CD=13,AD=5,∴BE边上的高AC=12,AB边上的高![]() ,AE边上的高
,AE边上的高![]() .
.

练习册系列答案
相关题目