��Ŀ����
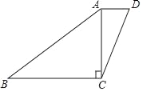
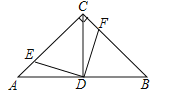
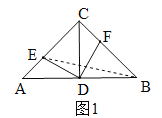
����Ŀ����ͼ���ڡ�ABC�У���ACB��90�㣬AC��BC��AB��2��CD�DZ�AB�ĸ��ߣ�����E�ӵ�A��������ÿ��1����λ���ٶ�������AC�˶���ͬʱ������F�ӵ�C����������ͬ���ٶ�������CB�˶�����E���˶�ʱ��Ϊt��s����t��0����
��1��AE���� �����ú�t�Ĵ���ʽ��ʾ������BCD�Ĵ�С���� ���ȣ�
��2����E�ڱ�AC���˶�ʱ����֤����ADE�ա�CDF��
��3����E�ڱ�AC���˶�ʱ�����EDF�Ķ�����
��4������BE����CE��ADʱ��ֱ��д��t��ֵ�ʹ�ʱBE��Ӧ��ֵ��

���𰸡���1��t��45����2�������������3��90������4��t��ֵΪ![]() ��1��
��1��![]() +1��BE=
+1��BE=![]() ��
��
��������
��1�����ݵ���ֱ�������ε����ʼ��ɽ�����⣻
��2������SAS����֤����ADE�ա�CDF��
��3���ɡ�ADE�ա�CDF�������Ƴ���ADE=��CDF���Ƴ���EDF=��ADC=90�㣻
��4�����������ηֱ���⼴�ɽ�����⣮
��1�������⣺AE=t��
��CA=CB����ACB=90�㣬CD��AB�����BCD=��ACD=45�㣮
�ʴ�Ϊ��t��45��
��2���ߡ�ACB=90�㣬CA=CB��CD��AB����CD=AD=BD�����A=��DCB=45�㣮
��AE=CF�����ADE�ա�CDF��SAS����
��3���ߵ�E�ڱ�AC���˶�ʱ����ADE�ա�CDF�����ADE=��CDF�����EDF=��ADC=90�㣮
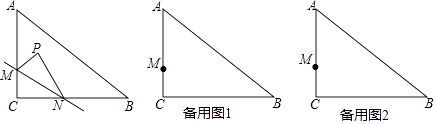
��4���ٵ���E��AC����ʱ����ͼ1����Rt��ACB�У��ߡ�ACB=90�㣬AC=CB��AB=2��CD��AB����CD=AD=DB=1��AC=BC![]() ��
��
��CE=CD=1����AE=AC��CE![]() 1����t
1����t![]() 1��
1��
��BC=![]() ����BE=
����BE=![]() =
=![]() =
=![]() ��
��
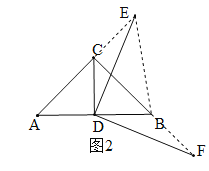
�ڵ���E��AC���ӳ�����ʱ����ͼ2��AE=AC+EC![]() 1����t
1����t![]() 1��
1��
��BC=![]() ����BE=
����BE=![]() =
=![]() =
=![]() ��
��
��������������������t��ֵΪ![]() 1��
1��![]() 1��BE=
1��BE=![]() ��
��