题目内容
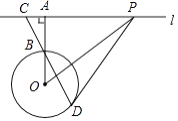
【题目】如图,AB是⊙O的弦,C是劣弧 ![]() 的中点,连BO并延长交⊙O于点D,连接CA,CB,AB与CD交于点F,已知CF=1,FD=2.
的中点,连BO并延长交⊙O于点D,连接CA,CB,AB与CD交于点F,已知CF=1,FD=2. 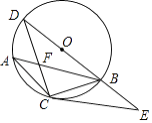
(1)求CB的长;
(2)延长DB到E,使BE=OB,连接CE,求证:CE是⊙O的切线.
【答案】
(1)解:∵C是劣弧 ![]() 的中点,
的中点,
∴∠1=∠2,
∵∠1=∠D,
∴∠2=∠D,
∵∠BCF=∠DCB,
∴△BCF∽△DCB,
∴ ![]() ,
,
∴BC2=CFCD=1×3=3,
∴BC= ![]() ;
;
(2)解:∵BD是⊙O的直径,
∴∠BCD=90°,
∴BD2=BC2+CD2=12,
∴BD=2 ![]() ,
,
∴OB=BE=BC,
连接OC,

∴∠OCE=90°,
∴OC⊥CE,
∴CE是⊙O的切线.
【解析】(1)由C是劣弧 ![]() 的中点,得到∠1=∠2,等量代换得到∠2=∠D,根据相似三角形的性质即可得到结论;(2)由BD是⊙O的直径,得到∠BCD=90°,根据勾股定理得到BD=2
的中点,得到∠1=∠2,等量代换得到∠2=∠D,根据相似三角形的性质即可得到结论;(2)由BD是⊙O的直径,得到∠BCD=90°,根据勾股定理得到BD=2 ![]() ,证得OB=BE=BC,连接OC,推出OC⊥CE,即可得到结论.
,证得OB=BE=BC,连接OC,推出OC⊥CE,即可得到结论.
【考点精析】掌握切线的判定定理和相似三角形的判定与性质是解答本题的根本,需要知道切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

【题目】现要把192吨物资从我市运往甲、乙两地,用大、小两种货车共18辆恰好能一次性运完这批物资.已知这两种货车的载重量分别为14吨/辆和8吨/辆,运往甲、乙两地的运费如表:
运往地 | 甲地(元/辆) | 乙地(元/辆) |
大货车 | 720 | 800 |
小货车 | 500 | 650 |
(1)求这两种货车各用多少辆?
(2)如果安排10辆货车前往甲地,其余货车前往乙地,其中前往甲地的大货车为a辆,前往甲、乙两地的总运费为w元,求出w与a的函数关系式;
(3)在(2)的条件下,若运往甲地的物资部少于96吨,请你设计出使总运费最低的货车调配方案,并求出最少总运费.