题目内容
【题目】填空,完成下列说理过程
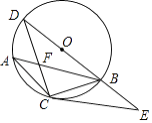
如图,∠AOB=90°,∠COD=90°,OA平分∠DOE,若∠BOC=20°,求∠COE的度数
解:因为∠AOB=90°.
所以∠BOC+∠AOC=90°
因为∠COD=90°
所以∠AOD+∠AOC=90°.
所以∠BOC=∠AOD. ( )
因为∠BOC=20°.
所以∠AOD=20°.
因为OA平分∠DOE
所以∠ =2∠AOD= °. ( )
所以∠COE=∠COD﹣∠DOE= °

【答案】同角的余角相等,DOE,40°,角平分线的定义,50°.
【解析】
根据余角的性质先求出∠AOD=∠BOC,再根据角平分线的定义求出∠DOE的度数,再根据∠COE=∠COD﹣∠DOE即可求得答案.
因为∠AOB=90°,
所以∠BOC+∠AOC=90°,
因为∠COD=90°,
所以∠AOD+∠AOC=90°,
所以∠BOC=∠AOD(同角的余角相等),
因为∠BOC=20°,
所以∠AOD=20°,
因为OA平分∠DOE,
所以∠DOE=2∠AOD=40°(角平分线的定义),
所以∠COE=∠COD﹣∠DOE=50°,
故答案为:同角的余角相等,DOE,40°,角平分线的定义,50°.

练习册系列答案
相关题目