题目内容
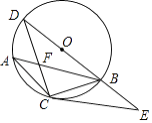
【题目】如图,直线l与⊙O相离,过点O作OA⊥l,垂足为A,OA交⊙O于点B,点C在直线l上,连接CB并延长交⊙O于点D,在直线l上另取一点P,使∠PCD=∠PDC. 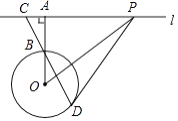
(1)求证:PD是⊙O的切线;
(2)若AC=1,AB=2,PD=6,求⊙O的半径r和△PCD的面积.
【答案】
(1)解:连接OD,
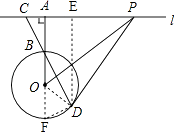
∴∠ABC=∠OBD=∠ODB,
∵OA⊥l,
∴∠PCD+∠ABC=90°,
∴∠PCD+∠ODB=90°,
∵∠PCD=∠PDC,
∴∠PDC+∠ODB=90°,即∠ODP=90°,
∴PD是⊙O的切线;
(2)解:∵∠PCD=∠PDC,
∴PC=PD=6,
∴PA=5,
设OB=OF=OD=r,
由PA2+AO2=PD2+OD2可得52+(2+r)2=62+r2,
解得:r= ![]() ,
,
延长AO交⊙O于点F,连接DF,
∵∠ABC=∠DBF、∠BAC=∠BDF=90°,
∴△ABC∽△DBF,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴DB= ![]() ,
,
过点D作DE⊥PC于点E,
∴△CAB∽△CED,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得:DE= ![]() ,
,
∴S△PCD= ![]() PCDE=
PCDE= ![]() ×6×
×6× ![]() =
= ![]() .
.
【解析】(1)连接OD,知∠ABC=∠OBD=∠ODB,由∠PCD+∠ABC=90°知∠PCD+∠ODB=90°,结合∠PCD=∠PDC可得∠ODP=90°,即可得证;(2)由∠PCD=∠PDC知PC=PD=6、PA=5,根据PA2+AO2=PD2+OD2可得r= ![]() ;延长AO交⊙O于点F,连接DF,证△ABC∽△DBF得
;延长AO交⊙O于点F,连接DF,证△ABC∽△DBF得 ![]() =
= ![]() ,即可知DB=
,即可知DB= ![]() ,作DE⊥PC于点E,由△CAB∽△CED知
,作DE⊥PC于点E,由△CAB∽△CED知 ![]() =
= ![]() ,求得DE=
,求得DE= ![]() ,从而求得△PCD的面积.
,从而求得△PCD的面积.
【考点精析】利用切线的判定定理对题目进行判断即可得到答案,需要熟知切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.

 口算题天天练系列答案
口算题天天练系列答案