题目内容
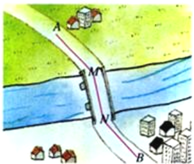
【题目】如图,A 和 B 两地在一条河的两岸,现要在河上造一座桥 MN.桥造在何处才能使从 A 到 B 的路径 AMNB 最短?在下图中画出路径,不写画法但要说明理由.(假定河的两岸是平行的直线,桥要与河垂直.)
【答案】见解析
【解析】
虽然A、B两点在河两侧,但连接AB的线段不垂直于河岸.关键在于使AM+BN最短,但AM与BN未连起来,要利用线段公理就要想办法使M和N重合起来,利用平行四边形的特征可以实现这一目的.
解:如图,作 BB'垂直于河岸 GH,使 BB′等于河宽, 连接 AB′,与河岸 EF 相交于 M,作 MN⊥GH,
则 MN∥BB′且 MN=BB′,
于是 MNBB′为平行四边形,故 NB=MB′.
根据“两点之间线段最短”,AB′最短,即 AM+BN 最短.
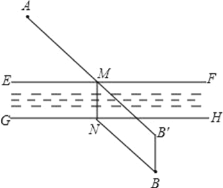
故桥建立在 MN 处符合题意.

练习册系列答案
相关题目