Question

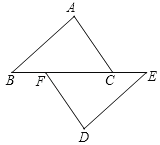
【题目】如图，点B、F、C、E在同一条直线上，点A、D在直线BC的异侧，AB=DE，AC=DF，BF=EC．

（1）求证：△ABC≌△DEF；

（2）若∠BFD=150°，求∠ACB的度数．

Answer 1

【答案】（1）见解析；（2）30°

【解析】

（1）根据BF=EC，可以得到BC=EF，然后根据题目中的条件，利用全等三角形的判定即可证明结论成立；

（2）根据邻补角互补和全等三角形的性质可以得到∠ACB的度数．

（1）∵BF=EC，∴BF+FC=EC+FC，∴BC=EF．

在△ABC和△DEF中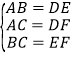，∵，∴△ABC≌△DEF（SSS）；

（2）∵∠BFD=150°，∠BFD+∠DFE=180°，∴∠DFE=30°．

由（1）知：△ABC≌△DEF，∴∠ACB=∠DFE，∴∠ACB=30°．