��Ŀ����
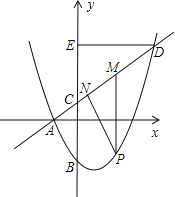
����Ŀ����ͼ��������y=![]() x2+bx+c��x�ύ�ڵ�A����2��0������y���ڵ�B��0��
x2+bx+c��x�ύ�ڵ�A����2��0������y���ڵ�B��0��![]() ����ֱ��y=kx
����ֱ��y=kx![]() ����A��y�ύ�ڵ�C���������ߵ���һ��������D��
����A��y�ύ�ڵ�C���������ߵ���һ��������D��
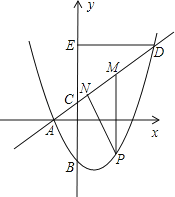
��1����������y=![]() x2+bx+c��ֱ��y=kx
x2+bx+c��ֱ��y=kx![]() �Ľ���ʽ��
�Ľ���ʽ��
��2�����P��ֱ��AD�·�����������һ���㣨�����A��D�غϣ�������P��y���ƽ���ߣ���ֱ��AD�ڵ�M����DE��y���ڵ�E��̽�����Ƿ���������ĵ�P��ʹ�ı���PMEC��ƽ���ı��Σ��������������P�����ꣻ�������ڣ���˵�����ɣ�
��3���ڣ�2���������£���PN��AD�ڵ�N������PMN���ܳ�Ϊm����P�ĺ�����Ϊx����m��x�ĺ�����ϵʽ�������m�����ֵ��
���𰸡���1��y=![]() x2��
x2��![]() x��
x��![]() ��y=
��y=![]() x+
x+![]() ����2��P�������ǣ�2����3���ͣ�4����
����2��P�������ǣ�2����3���ͣ�4����![]() �������ɼ���������3����x=3ʱ��m�����ֵ��15��
�������ɼ���������3����x=3ʱ��m�����ֵ��15��
��������
�����������1���ѵ�A��B������ֱ���������߽���ʽ���г�����b��c�ķ����飬ͨ���ⷽ����������b��c��ֵ���ѵ�A���������һ�κ�������ʽ���г�����k�ķ��̣�ͨ���ⷽ�����k��ֵ��
��2������ƽ���ı��ε�������֪EC=PM�������D�������ǣ�8��7![]() ������C�������ǣ�0��
������C�������ǣ�0��![]() ������CE=6����P�������ǣ�x��
������CE=6����P�������ǣ�x��![]() x2��
x2��![]() x��
x��![]() ������M�������ǣ�x��
������M�������ǣ�x��![]() x+
x+![]() ����
����
��PM=��![]() x+
x+![]() ������
������![]() x2��
x2��![]() x��
x��![]() ��=��
��=��![]() x2+
x2+![]() x+4��������EC=PM�õ���
x+4��������EC=PM�õ���![]() x2+
x2+![]() x+4=6��ͨ���ⷽ����õ�P�������ǣ�2����3���ͣ�4����
x+4=6��ͨ���ⷽ����õ�P�������ǣ�2����3���ͣ�4����![]() ����
����
��3��ͨ��������������PMN�ס�CDE��������֪��![]() =
=![]() ����������ݴ��벢�������Եó�m��x�ĺ�����ϵʽ�ǣ�m=��
����������ݴ��벢�������Եó�m��x�ĺ�����ϵʽ�ǣ�m=��![]() x2+
x2+![]() x+
x+![]() =��
=��![]() ��x��3��2+15��
��x��3��2+15��
�������ߵ����ʿ��Եõ���m�����ֵ����x=3ʱ��m�����ֵ��15��
�⣺��1����y=![]() x2+bx+c������A����2��0����B��0��
x2+bx+c������A����2��0����B��0��![]() ��
��
���ɴ˵�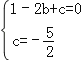 �����
�����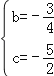
�������ߵĽ���ʽ��y=![]() x2��
x2��![]() x��
x��![]() ��
��
��ֱ��y=kx![]() ������A����2��0��
������A����2��0��
����2k+![]() =0��
=0��
��ã�k=![]() ��
��
��ֱ�ߵĽ���ʽ�� y=![]() x+
x+![]() ��
��
��2������D�������ǣ�8��7![]() ������C�������ǣ�0��
������C�������ǣ�0��![]() ����
����
��CE=6��
��P�������ǣ�x��![]() x2��
x2��![]() x��
x��![]() ������M�������ǣ�x��
������M�������ǣ�x��![]() x+
x+![]() ��
��
��Ϊ��P��ֱ��AD���·���
��ʱPM=��![]() x+
x+![]() ������
������![]() x2��
x2��![]() x��
x��![]() ��=��
��=��![]() x2+
x2+![]() x+4��
x+4��
����PM��y�ᣬҪʹ�ı���PMEC��ƽ���ı��Σ�����PM=CE��
����![]() x2+
x2+![]() x+4=6
x+4=6
��������̵ã�x1=2��x2=4��
��x=2ʱ��y=��3��
��x=4ʱ��y=��![]() ��
��
��ˣ�ֱ��AD�·����������ϴ��������ĵ�P��ʹ�ı���PMEC��ƽ���ı��Σ�
��P�������ǣ�2����3���ͣ�4����![]() ����
����
��3����Rt��CDE�У�DE=8��CE=6 �ɹ��ɶ����ã�DC=![]() =10
=10
���CDE���ܳ���24��
��PM��y�ᣬ���PMN=��DCE��
�ߡ�PNM=��DEC=90�������PMN�ס�CDE��
��![]() =
=![]() ����
���� ![]() =
=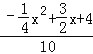 ��
��
���������ã�m��x�ĺ�����ϵʽ�ǣ�m=��![]() x2+
x2+![]() x+
x+![]() ��
��
m=��![]() x2+
x2+![]() x+
x+![]() =��
=��![]() ��x��3��2+15��
��x��3��2+15��
����![]() ��0��
��0��
��m�����ֵ����x=3ʱ��m�����ֵ��15��