题目内容
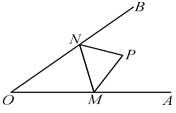
【题目】如图,![]() ,点
,点![]() 是
是![]() 内的一定点,点
内的一定点,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上移动,当
上移动,当![]() 的周长最小时,
的周长最小时,![]() 的度数为( )
的度数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
分别作点P关于OA、OB的对称点P1、P2,连接P1、P2,交OA于M,交OB于N,△PMN的周长最小值等于P1P2的长,然后依据等腰△OP1P2中,∠OP1P2+∠OP2P1=180°﹣2α,即可得出∠MPN=∠OPM+∠OPN=∠OP1M+∠OP2N=180°﹣2α.
分别作点P关于OA、OB的对称点P1、P2,连接P1、P2,交OA于M,交OB于N,则OP1=OP=OP2,∠OP1M=∠MPO,∠NPO=∠NP2O.
根据轴对称的性质可得MP=P1M,PN=P2N,∴△PMN的周长的最小值=P1P2,
由轴对称的性质可得∠P1OP2=2∠AOB=2α,∴等腰△OP1P2中,∠OP1P2+∠OP2P1=180°﹣2α,∴∠MPN=∠OPM+∠OPN=∠OP1M+∠OP2N=∠OP1P2+∠OP2P1=180°﹣2α.
故选B.


练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目