题目内容
【题目】已知A(x,0),B(0,y),且x,y满足![]() ,且点A与点C关于y轴对称.
,且点A与点C关于y轴对称.
(1)求C坐标;
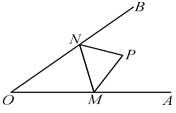
(2)如图1,点D在射线BA上,连接CD,若b=4,∠D=![]() ∠CBA,求CD长
∠CBA,求CD长
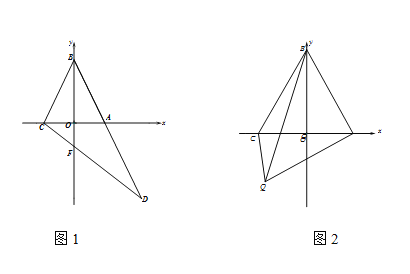
(3)如图2,如图2,BC=2OC,点Q是平面内一点,连接 QB,QC,QA,若QB=m,QC=OA,求AQ最大值.
【答案】(1)(-a,0);(2)16;(3)3a.
【解析】
(1)将式子进行配方,利用平方式的非负性得到x和y的值,然后根据点A与点C关于y轴对称得到点C的坐标;
(2)过点C作x轴的垂线交AB的延长线于点G,可得到OB为△ACG的中位线,再通过∠D=![]() ∠CBA得到CD=CG,即可得到CD的长度;
∠CBA得到CD=CG,即可得到CD的长度;
(3)由于QC=OA,所以点Q是在以C为圆心CQ为半径的圆上运动,当A、C、Q三点在同一直线上且Q在C点左侧时,AQ取得最大值,由此求得AQ最大为3a.
解:(1)∵![]()
∴![]()
∴![]() ,
,
∴A(a,0),B(0,2b),
又∵点A与点C关于y轴对称,
∴C点坐标为(-a,0).
(2)过点C作x轴的垂线交AB的延长线于点G,
易得OB∥CG,O为AC的中点,
∴OB为△ACG的中位线,即![]() ,
,
∵b=4,
∴OB=2b=8,CG=2OB=16,
由点A与点C关于y轴对称,可得∠ABO=∠CBO=![]() ∠DBC,
∠DBC,
又∵∠D=![]() ∠CBA,
∠CBA,
∴∠D=∠ABO,
由OB∥CG,可知∠ABO=∠CGB,
∴∠D=∠CGB,
∴CD=CG=16.
(3)由以上可得,A(a,0),C(-a,0),
∵QC=OA,
∴所以点Q是在以C为圆心CQ为半径的圆上运动,
当A、C、Q三点在同一直线上且Q在C点左侧时,AQ取得最大值,
此时AQ=a+a+a=3a.

练习册系列答案
相关题目