Question

【题目】如图，AB为⊙O的直径，直线CD切⊙O于点D，AM⊥CD于点M，BN⊥CD于N．
（1）求证：∠ADC=∠ABD；
（2）求证：AD2=AMAB；
（3）若AM= ，sin∠ABD= ，求线段BN的长．

Answer 1

【答案】
（1）证明：连接OD，

∵直线CD切⊙O于点D，

∴∠CDO=90°，

∵AB为⊙O的直径，

∴∠ADB=90°，

∴∠1+∠2=∠2+∠3=90°，

∴∠1=∠3，

∵OB=OD，

∴∠3=∠4，

∴∠ADC=∠ABD；

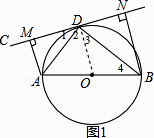
（2）证明：∵AM⊥CD，

∴∠AMD=∠ADB=90°，

∵∠1=∠4，

∴△ADM∽△ABD，

∴ ，

∴AD2=AMAB；

（3）解：∵sin∠ABD= ，

∴sin∠1= ，

∵AM= ，

∴AD=6，

∴AB=10，

∴BD= =8，

∵BN⊥CD，

∴∠BND=90°，

∴∠DBN+∠BDN=∠1+∠BDN=90°，

∴∠DBN=∠1，

∴sin∠NBD= ，

∴DN= ，

∴BN= = ．

【解析】（1）连接OD，由切线的性质和圆周角定理即可得到结果；（2）由已知条件证得△ADM∽△ABD，即可得到结论；（3）根据三角函数和勾股定理代入数值即可得到结果．