题目内容
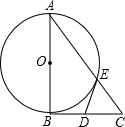
如图所示,△ABC是直角三角形,∠ABC=90°,以AB为直径的⊙O交AC于点E,点D是BC边的中点,连接DE.
(1)求证:DE与⊙O相切;
(2)若⊙O的半径为
,DE=3,求AE.
(1)求证:DE与⊙O相切;
(2)若⊙O的半径为
| 3 |

(1)证明:连接OE,BE,
∵AB是直径.
∴BE⊥AC.
∵D是BC的中点,
∴DC=DB.
∴∠DBE=∠DEB.
又OE=OB,
∴∠OBE=∠OEB.
∴∠DBE+∠OBE=∠DEB+∠OEB.
即∠ABD=∠OED.
但∠ABC=90°,
∴∠OED=90°.
∴DE是⊙O的切线.
(2)法1:∵∠ABC=90°,AB=2
,BC=2DE=6,
∴AC=4
.
∴BE=3.
∴AE=
;
法2:∵AC=
=
=4
(8分)
∴BE=
=
=3(10分)
∴AE=
=
=
.(12分)

∵AB是直径.
∴BE⊥AC.
∵D是BC的中点,
∴DC=DB.
∴∠DBE=∠DEB.
又OE=OB,
∴∠OBE=∠OEB.
∴∠DBE+∠OBE=∠DEB+∠OEB.
即∠ABD=∠OED.
但∠ABC=90°,
∴∠OED=90°.
∴DE是⊙O的切线.
(2)法1:∵∠ABC=90°,AB=2
| 3 |
∴AC=4
| 3 |
∴BE=3.
∴AE=
| 3 |
法2:∵AC=
| AB2+BC2 |
(2
|
| 3 |
∴BE=
| AB•BC |
| AC |
2
| ||
4
|
∴AE=
| AB2-BE2 |
| 12-9 |
| 3 |


练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 ,作⊙O′的切线PE切⊙O′于点E.若PC=4,CD=8,⊙O的半径为5.
,作⊙O′的切线PE切⊙O′于点E.若PC=4,CD=8,⊙O的半径为5.

