题目内容
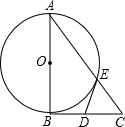
如图，AC是⊙O的直径，PA切⊙O于点A，点B是⊙O上的一点，且∠BAC=30°，∠APB=60°．求证：PB是⊙O的切线．
证明：连接OB，
∵PA切⊙O于A，
∴∠PAO=90°，
∵∠BAC=90°，弧BC对的圆周角是∠BAC，对的圆心角是∠COB，
∴∠COB=2∠BAC=60°，
∴∠AOB=180°-60°=120°，
∵∠APB=60°，
∴在四边形AOBP中，∠PBO=360°-90°-60°-120°=90°，
即OB⊥PB，
∵OB是半径，
∴PB是⊙O的切线．
∵PA切⊙O于A，
∴∠PAO=90°，
∵∠BAC=90°，弧BC对的圆周角是∠BAC，对的圆心角是∠COB，
∴∠COB=2∠BAC=60°，
∴∠AOB=180°-60°=120°，
∵∠APB=60°，
∴在四边形AOBP中，∠PBO=360°-90°-60°-120°=90°，
即OB⊥PB，
∵OB是半径，
∴PB是⊙O的切线．
练习册系列答案
相关题目
点F，E为垂足．
写出自变量x的取值范围．
