Question

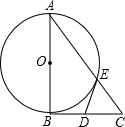
如图，⊙O的半径OC与直径AB垂直，点P在OB上运动（点O、B除外），CP的延长线交⊙O于点D，在OB的延长线上取点E，使ED=EP．
（1）求证：ED是⊙O的切线；
（2）当OC=2，ED=2

3

时，求∠E的正切值tanE和图中阴影部分的面积S（结果保留无理数）．

Answer 1

（1）证明：连接OD，
∵OD是圆的半径，
∴OD=OC．
∴∠CDO=∠DCO．
∵OC⊥AB，
∴∠COP=90°．
∵在Rt△OPC中，∠CPO+∠PCO=90°，
∵ED=EP，
∴∠EDP=∠EPD=∠CPO．
∴∠EDO=∠EDP+∠CDO=∠CPO+∠DCO=90°．
∴ED⊥OD，即ED是圆的切线．

（2）∵OD=OC=2，ED=2

3

，
∴tan∠E=

OD

ED

=

3

3

．
∴∠E=30°，∠DOB=60°．
∴S_阴影=S_△ODE-S_扇形=

1

2

×2×2

3

-

60π×22

360

=2

3

-

2

3

π（平方单位）．