题目内容
【题目】如图,平面直角坐标系xOy中,点C(3,0),函数y= ![]() (k>0,x>0)的图象经过OABC的顶点A(m,n)和边BC的中点D.
(k>0,x>0)的图象经过OABC的顶点A(m,n)和边BC的中点D.
(1)求m的值;
(2)若△OAD的面积等于6,求k的值;
(3)若P为函数y═ ![]() (k>0,x>0)的图象上一个动点,过点P作直线l⊥x轴于点M,直线l与x轴上方的OABC的一边交于点N,设点P的横坐标为t,当
(k>0,x>0)的图象上一个动点,过点P作直线l⊥x轴于点M,直线l与x轴上方的OABC的一边交于点N,设点P的横坐标为t,当 ![]() 时,求t的值.
时,求t的值.
【答案】
(1)
解:∵点C(3,0),OABC的顶点A(m,n),
∴B(m+3,n),
∴D( ![]() +3,
+3, ![]() ),
),
∵函数y= ![]() (k>0,x>0)的图象经过OABC的顶点A(m,n)和边BC的中点D,
(k>0,x>0)的图象经过OABC的顶点A(m,n)和边BC的中点D,
∴mn=k, ![]() ,
,
∴m=2
(2)
解:∵点D是平行四边形BC中点,
∴S平行四边形OABC=2S△OAD=12,
∵S平行四边形OABC=3×n=12,
∴n=4,
由(1)知,m=2,
∴k=mn=8
(3)
解:①如图1,点N在OA上,
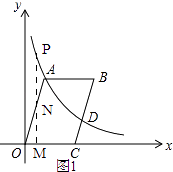
由(1)知,m=2,
∴A(2,n).
即0<t<2
直线OA的解析式为y= ![]() x,
x,
设点P的横坐标为t,
∴P(t, ![]() ),
),
∵过点P作直线l⊥x轴于点M.
∴N(t, ![]() t),M(t,0),
t),M(t,0),
∴PN= ![]() ﹣
﹣ ![]() t,PM=
t,PM= ![]() ,
,
∵ ![]() ,
,
∴ ![]() =4(
=4( ![]() ﹣
﹣ ![]() t),
t),
∴t= ![]() 或t=﹣
或t=﹣ ![]() (舍),
(舍),
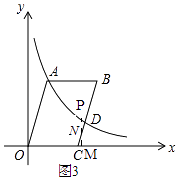
②如图2,

当点N在AB上时,
由(1)知,B(5,n),
∴2≤t≤3
由题意知,P(t, ![]() ).N(t,n),M(t,0),
).N(t,n),M(t,0),
∵ ![]() ,
,
∴4(n﹣ ![]() )=
)= ![]() ,
,
∴t= ![]() ,
,
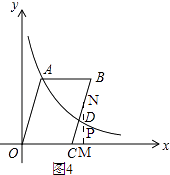
当点N在BC上时,(3<t≤5)
∵B(5,n),C(3,0),
∴直线BC解析式为y= ![]() x﹣
x﹣ ![]() ,
,
∴P(t, ![]() ),N(t,
),N(t, ![]() t﹣
t﹣ ![]() ),M(t,0),
),M(t,0),
∵ ![]() ,
,
∴4| ![]() t﹣
t﹣ ![]() ﹣
﹣ ![]() |=
|= ![]() ,
,
∴t= ![]() 或t=
或t= ![]() (舍)或t=
(舍)或t= ![]() 或t=
或t= ![]() (舍)
(舍)
∴t的值为 ![]() ,
, ![]() ,
, ![]() 或
或 ![]()
【解析】(1)根据平行四边形的性质确定出B的坐标从而确定出D的坐标,而点A,D在反比例函数图象上,建立方程求出m,(2)根据三角形OAD的面积是平行四边形OABC面积的一半,确定出n即可;(3)根据平行四边形的性质和双曲线的性质,确定出PM,ON即可.
【考点精析】根据题目的已知条件,利用反比例函数的图象和反比例函数的性质的相关知识可以得到问题的答案,需要掌握反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点;性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大.

 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案