Question

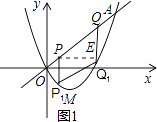
【题目】如图，在平面直角坐标系xOy中，一次函数y=x与二次函数y=x2+bx的图象相交于O、A两点，点A（3，3），点M为抛物线的顶点．

（1）求二次函数的表达式；
（2）长度为2 的线段PQ在线段OA（不包括端点）上滑动，分别过点P、Q作x轴的垂线交抛物线于点P1、Q1 ， 求四边形PQQ1P1面积的最大值；
（3）直线OA上是否存在点E，使得点E关于直线MA的对称点F满足S△AOF=S△AOM？若存在，求出点E的坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）

解：把点A（3，3）代入y=x2+bx中，

得：3=9+3b，解得：b=﹣2，

∴二次函数的表达式为y=x2﹣2x

（2）

解：设点P在点Q的左下方，过点P作PE⊥QQ1于点E，如图1所示．

∵PE⊥QQ1，QQ1⊥x轴，

∴PE∥x轴，

∵直线OA的解析式为y=x，

∴∠QPE=45°，

∴PE= PQ=2．

设点P（m，m）（0＜m＜1），则Q（m+2，m+2），P1（m，m2﹣2m），Q1（m+2，m2+2m），

∴PP1=3m﹣m2，QQ1=2﹣m2﹣m，

∴ = （PP1+QQ1）PE=﹣2m2+2m+2=﹣2 + ，

∴当m= 时， 取最大值，最大值为

（3）

解：存在．

如图2中，①点E的对称点为F，EF与AM交于点G，连接OM、MF、AF、OF．

∵S△AOF=S△AOM，

∴MF∥OA，

∵EG=GF， = ，

∴AG=GM，

∵M（1，﹣1），A（3，3），

∴点G（2，1），

∵直线AM解析式为y=2x﹣3，

∴线段AM的中垂线EF的解析式为y=﹣ x+2，

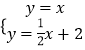由 解得 ，

∴点E坐标为（ ， ）．

②设E关于点A的对称点E′，E′关于AM的对称点F′，根据对称性可知，△OAF′与△AOF的面积相等，

此时E′（ ， ），

综上所述满足条件的点E坐标（ ， ）或（ ， ）

【解析】（1）把点A（3，3）代入y=x2+bx中，即可解决问题．（2）设点P在点Q的左下方，过点P作PE⊥QQ1于点E，如图1所示．设点P（m，m）（0＜m＜1），则Q（m+2，m+2），P1（m，m2﹣2m），Q1（m+2，m2+2m），构建二次函数，利用二次函数性质即可解决问题．（3）存在，首先证明EF是线段AM的中垂线，利用方程组求交点E坐标，再根据对称性E关于点A的对称点E′也符合条件，求出E、E′坐标即可．
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能正确解答此题．