题目内容
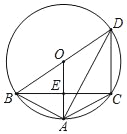
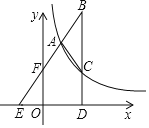
【题目】如图,在△ABC中,AB=AC,BC⊥x轴,垂足为D,边AB所在直线分别交x轴、y轴于点E、F,且AF=EF,反比例函数y=![]() 的图象经过A、C两点,已知点A(2,n).
的图象经过A、C两点,已知点A(2,n).
(1)求AB所在直线对应的函数表达式;(2)求点C的坐标.
【答案】(1)y=![]() x+3;(2)C(4,3).
x+3;(2)C(4,3).
【解析】
(1)先根据点A(2,n)在反比例函数y=![]() 的图象上,得出点A的坐标,作AH⊥OD于H.由△EFO∽△EAH,可得
的图象上,得出点A的坐标,作AH⊥OD于H.由△EFO∽△EAH,可得![]() ,由此求出E、F坐标,再利用待定系数法即可解决问题;
,由此求出E、F坐标,再利用待定系数法即可解决问题;
(2)作AG⊥BD于G.则四边形AGDH是矩形,根据等腰三角形的性质证出BG=CG,构建方程即可解决问题;
解:(1)把A(2,n)代入y=![]() ,得到n=6,
,得到n=6,
作AH⊥OD于H.
∴OH=2,AH=6,
∵△EFO∽△EAH,
∴![]() ,
,
∵EF=AF,
∴![]() ,
,
∴EO=2,FO=3,
∴E(﹣2,0),F(0,3),
设直线AB的解析式为y=kx+b,则有![]() ,
,
解得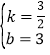 ,
,
∴直线AB的解析式为y=![]() x+3.
x+3.
(2)作AG⊥BD于G.则四边形AGDH是矩形,
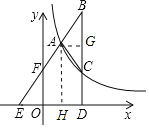
∴DG=AH=6,设C(a,![]() ),则B(a,
),则B(a,![]() a+3),
a+3),
∴CD=![]() ,BG=
,BG=![]() a+3﹣6=
a+3﹣6=![]() a﹣3,GC=6﹣
a﹣3,GC=6﹣![]() ,
,
∵AB=AC,AG⊥BC,
∴BG=CG,
∴![]() a﹣3
a﹣3![]() ,
,
整理得:a2﹣6a+8=8,∴a=4或2,
∵A(2,6)
∴C(4,3)

 阅读快车系列答案
阅读快车系列答案【题目】某校教师开展了“练一手好字”的活动,校委会对部分教师练习字帖的情况进行了问卷调查,问卷设置了“柳体”、“颜体”、”欧体“和”其他“类型,每位教师仅能选一项,根据调查的结果绘制了如下统计表:
类别 | 柳体 | 颜体 | 欧体 | 其他 | 合计 |
人数 | 4 | 10 | 6 | ||
占的百分比 | 0.5 | 0.25 | 1 |
根据图表提供的信息解答下列问题:
(1)这次问卷调查了多少名教师?
(2)请你补全表格.
(3)在调查问卷中,甲、乙、丙、丁四位教师选择了“柳体”,现从以上四位教师中任意选出2名教师参加学校的柳体兴趣小组,请你用画树状图或列表的方法,求选出的2人恰好是乙和丙两位教师的概率.
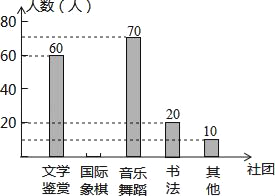
【题目】为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向.并将调查结果绘制成如下统计图表(不完整):
选择意向 | 文学鉴赏 | 国际象棋 | 音乐舞蹈 | 书法 | 其他 |
所占百分比 | a | 20% | b | 10% | 5% |
根据统计图表的信息,解答下列问题:
(1)求本次抽样调查的学生总人数及a、b的值;
(2)将条形统计图补充完整;
(3)若该校共有1300名学生,试估计全校选择“音乐舞蹈”社团的学生人数.