题目内容
【题目】如图,在矩形ABCD中,AB=8,AD=6,点P为矩形ABCD内一点,满足∠APB=90°,连结C、P两点,并延长CP交直线AB于点E.若点P是线段CE的中点,则BE=____.

【答案】![]()
【解析】
根据∠APB=90°可知点P在以AB为直径的![]() 上,然后分两种情况讨论:①当点E在点A左侧时,②当点E在线段AB上时;根据三角形中位线的判定和性质求出PQ,再利用勾股定理求出OQ,然后分情况求出BQ的长即可解决问题.
上,然后分两种情况讨论:①当点E在点A左侧时,②当点E在线段AB上时;根据三角形中位线的判定和性质求出PQ,再利用勾股定理求出OQ,然后分情况求出BQ的长即可解决问题.
解:∵∠APB=90°,
∴点P在以AB为直径的![]() 上,
上,
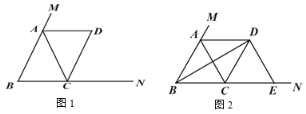
分两种情况:①如图1,当点E在点A左侧时,O为![]() 所在圆的圆心,连接PO,作PQ⊥AB于Q,
所在圆的圆心,连接PO,作PQ⊥AB于Q,
∵点P是线段CE的中点,PQ∥BC,
∴PQ是△EBC的中位线,
∴PQ=![]() ,
,
∵OP=OA=![]() ,
,
∴OQ=![]() ,
,
∴BQ=![]() ,
,
∴BE=2BQ=![]() ;
;
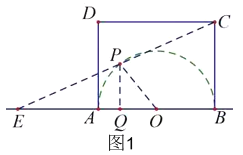
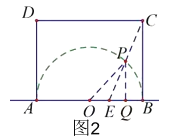
②如图2,当点E在线段AB上时,O为![]() 所在圆的圆心,连接PO,作PQ⊥AB于Q,
所在圆的圆心,连接PO,作PQ⊥AB于Q,
同①可得:OQ=![]() ,
,
∴BQ=![]() ,
,
∴BE=2BQ=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目