题目内容
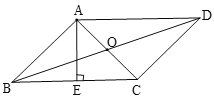
【题目】如图，平行四边形ABCD的对角线AC与BD相交于点O．
，垂足为E，AB=12，AC=10，BD=26，则AE的长为_________．
【答案】
【解析】
根据平行线对角线互相平分的性质可得OA、OB的长，根据勾股定理逆定理可得△BAO是直角三角形，∠BAO=90°，利用勾股定理可求出BC的长，利用面积法即可求出AE的长．
∵平行四边形ABCD的对角线AC与BD相交于点O，AC=10，BD=26，
∴OA=5，OB=13，
∵AB=12，122+52=132，
∴OB2=AB2+OA2，
∴△BAO是直角三角形，∠BAO=90°，
在Rt△BAC中，BC=
=
，
∵AE⊥BC，
∴S△ABC=
AB·AC=BC·AE，即12×10=×AE，
解得：AE=，
故答案为：
练习册系列答案
相关题目
