题目内容
【题目】在△ABC 中,AB=AC,点 M 在 BA 的延长线上,点 N 在 BC 的延长线上,过点 C 作CD∥AB 交∠CAM 的平分线于点 D.
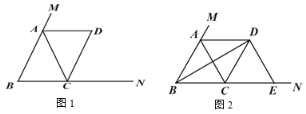
(1)如图 1,求证:四边形 ABCD 是平行四边形;
(2)如图 2,当∠ABC=60°时,连接 BD,过点 D 作 DE⊥BD,交 BN 于点 E,在不添加任何辅助线的情况下,请直接写出图 2 中四个三角形(不包含△CDE),使写出的每个三角形的面积与△CDE 的面积相等.
【答案】(1)见解析;(2)△ABC、△DBC、△ABD、△ACD.
【解析】
(1)根据等腰三角形的性质和三角形外角的性质可得∠CAM=2∠ABC,根据角平分线的定义可得∠CAM=2∠MAD,等量代换得到∠ABC=∠MAD,进而证得AD∥BC即可解决问题;
(2)首先证明平行四边形ABCD是菱形,然后证明△DCE是等边三角形,得到CE=CD=BC=AD,根据等底等高的三角形面积相等可得答案.
解:(1)∵AB=AC,
∴∠ABC=∠ACB,
∴∠CAM=∠ABC+∠ACB=2∠ABC,
∵AD是∠CAM 的平分线,
∴∠CAM=2∠MAD,
∴∠ABC=∠MAD,
∴AD∥BC,
∵CD∥AB,
∴四边形ABCD是平行四边形;
(2)∵∠ABC=60°,AB=AC,四边形ABCD是平行四边形,
∴△ABC是等边三角形,∠DCE=∠ABC=60°,
∴AB=BC,
∴平行四边形ABCD是菱形,
∴∠DBE=30°,
∵DE⊥BD,
∴∠DEB=60°,
∴△DCE是等边三角形,
∴CE=CD=BC=AD,
∵AD∥BC,
∴△ABC、△DBC、△ABD、△ACD的面积都与△CDE的面积相等.

练习册系列答案
相关题目