题目内容
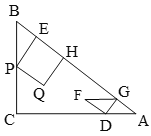
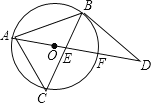
【题目】如图所示,以![]() 的边
的边![]() 为直径作
为直径作![]() ,点C在
,点C在![]() 上,
上,![]() 是
是![]() 的弦,
的弦,![]() ,过点C作
,过点C作![]() 于点F,交
于点F,交![]() 于点G,过C作
于点G,过C作![]() 交
交![]() 的延长线于点E.
的延长线于点E.
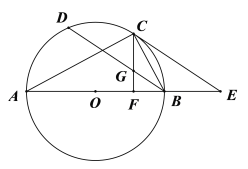
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]() ;
;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)见解析;(3)BE=![]() .
.
【解析】
(1)连接OC,由∠A=∠CBD可得![]() ,进而根据垂径定理可得OC⊥BD,然后根据CE∥BD即可推出OC⊥CE,问题即得解决;
,进而根据垂径定理可得OC⊥BD,然后根据CE∥BD即可推出OC⊥CE,问题即得解决;
(2)由AB为直径可得∠ACB=90°,然后根据同角的余角相等得出∠A=∠BCF,进而可得∠BCF=∠CBD,进一步即可证得结论;
(3)根据(2)的结论和30°角的直角三角形的性质可求得GF和BF的长,再在直角△CEF中利用30°角的直角三角形的性质可求得EF的长,进一步即可求出结果.
(1)证明:连接OC,如图,
∵∠A=∠CBD,∴![]() ,∴OC⊥BD,
,∴OC⊥BD,
∵CE∥BD,∴OC⊥CE,
∴CE是⊙O的切线;
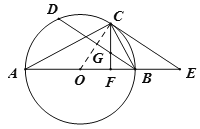
(2)证明:∵AB为直径,∴∠ACB=90°,
∵CF⊥AB,∴∠ACB=∠CFB=90°,
∵∠ABC=∠CBF,∴∠A=∠BCF,
∵∠A=∠CBD,∴∠BCF=∠CBD,
∴CG=BG;
(3)解:∵∠DBA=30°,![]() ,∴
,∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
∵CE∥BD,∴∠E=∠DBA=30°,
∴![]() ,
,
∴BE=![]() .
.

【题目】某年级共有150名女生,为了解该年级女生实心球成绩(单位:米)和一分钟仰卧起坐成绩(单位:个)的情况,从中随机抽取30名女生进行测试,获得了他们的相关成绩,并对数据进行整理、描述和分析.下面给出了部分信息.
a. 实心球成绩的频数分布表如下:
分组 |
|
|
|
|
|
|
频数 | 2 | m | 10 | 6 | 2 | 1 |
b. 实心球成绩在![]() 这一组的是:
这一组的是:
a7.0 7.0 7.0 7.1 7.1 7.1 7.2 7.2 7.3 7.3
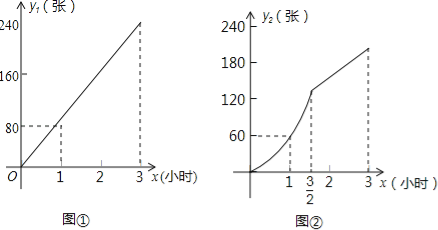
c. 一分钟仰卧起坐成绩如下图所示:
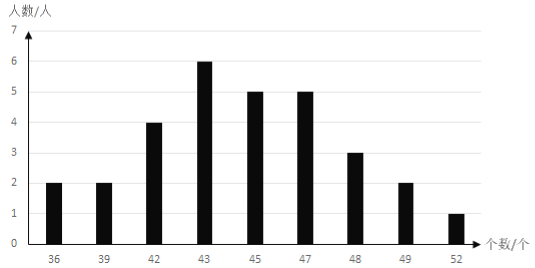
根据以上信息,回答下列问题:
(1) ①表中m的值为__________;
②一分钟仰卧起坐成绩的中位数为__________;
(2)若实心球成绩达到7.2米及以上时,成绩记为优秀.
①请估计全年级女生实心球成绩达到优秀的人数;
②该年级某班体育委员将本班在这次抽样测试中被抽取的8名女生的两项成绩的数据抄录如下:
女生代码 | A | B | C | D | E | F | G | H |
实心球 | 8.1 | 7.7 | 7.5 | 7.5 | 7.3 | 7.2 | 7.0 | 6.5 |
一分钟仰卧起坐 | * | 42 | 47 | * | 47 | 52 | * | 49 |
其中有3名女生的一分钟仰卧起坐成绩未抄录完整,但老师说这8名女生中恰好有4人两项测试成绩都达到了优秀,于是体育委员推测女生E的一分钟仰卧起坐成绩达到了优秀,你同意体育委员的说法吗?并说明你的理由.
【题目】某地政府计划为农户购买农机设备提供补贴.其中购买Ⅰ型、Ⅱ型设备农民所投资的金额与政府补贴的额度存在下表所示的函数对应关系.
型号 金额 | Ⅰ型设备 | Ⅱ型设备 | |||
投资金额x(万元) | x | 5 | x | 2 | 4 |
补贴金额y(万元) | y1=kx(k≠0) | 2 | y2=ax2+bx(a≠0) | 2.8 | 4 |
(1)分别求y1和y2的函数解析式;
(2)有一农户共投资10万元购买Ⅰ型、Ⅱ型两种设备,两种设备的投资均为整数万元,要想获得最大补贴金额,应该如何购买?能获得的最大补贴金额为多少?