题目内容
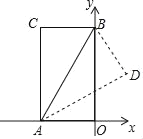
【题目】如图,抛物线y=![]() x2﹣3x+4与x轴交于A、B两点(A点在B点的左侧),交y轴于点C.
x2﹣3x+4与x轴交于A、B两点(A点在B点的左侧),交y轴于点C.
(1)A点坐标为 ,B点坐标为 ,C点坐标为 ;
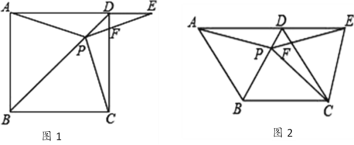
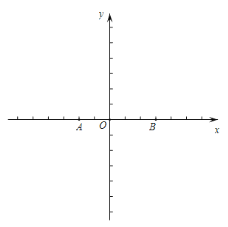
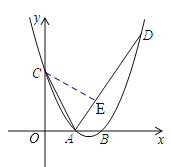
(2)如图1,D为B点右侧抛物线上一点,连接AD,若tan∠CAD=2,求D点坐标;
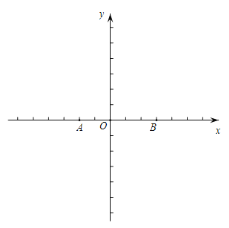
(3)E、F是对称轴右侧第一象限抛物线上的两动点,直线AE、AF分别交y轴于M、N,如图2.若OMON=2,直线EF上有且只有一点P到原点O的距离为定值,求出P点的坐标.

【答案】(1)A(2,0),B(4,0), C(0,4);(2)(![]() ,
,![]() );(3)P(4,﹣1)
);(3)P(4,﹣1)
【解析】
(1)令y=0解一元二次方程求出A、B点的坐标,令x=0,求出C点的坐标;
(2)过C点作CE⊥AD于点E,则tan∠CAE=2,先证明Rt△AOC≌Rt△AEC,再求出AD所在的直线解析式为y=![]() x﹣
x﹣![]() ,最后联立方程组求解D点坐标;
,最后联立方程组求解D点坐标;
(3)设yAE=k1x+b1,yAF=k2x+b2,根据已知可求得k1k2=![]() ,分别求出E与F点坐标,表示出EF所在直线解析式为:y=(k1+k2+1)x﹣(4k1+4k2+5),直线EF经过的定点即为P点.
,分别求出E与F点坐标,表示出EF所在直线解析式为:y=(k1+k2+1)x﹣(4k1+4k2+5),直线EF经过的定点即为P点.
(1)令y=![]() x2﹣3x+4=0,解得x1=2,x2=4,故A(2,0),B(4,0);令x=0,则y=4,所以C点的坐标为(0,4);
x2﹣3x+4=0,解得x1=2,x2=4,故A(2,0),B(4,0);令x=0,则y=4,所以C点的坐标为(0,4);
(2)如图,过C点作CE⊥AD于点E,则tan∠CAE=2,
由(1)知tan∠CAO=![]() =2,
=2,
∴∠CAE=∠CAO,
在Rt△AOC和Rt△AEC中,
∠CAE=∠CAO,
∠AOC=∠AEC=90°,
AC=AC,
∴Rt△AOC≌Rt△AEC(AAS)
∴CE=4,AE=2;
设E(m,n),
∴16=m2+(n﹣4)2,4=(m﹣2)2+n2,
∴m=2n,
∴m=![]() ,n=
,n=![]() ,
,
∴E(![]() ,
,![]() ),
),
设AD所在的直线解析式为y=kx+b,
把点A(2,0),E(![]() ,
,![]() )代入,
)代入,
解得,k=![]() ,b=
,b=![]() ,
,
∴y=![]() x﹣
x﹣![]() ,与y=
,与y=![]() x2﹣3x+4联立解得,x1=2,x2=
x2﹣3x+4联立解得,x1=2,x2=![]() ,
,
当x=![]() 时,y=
时,y=![]()
所以D点的坐标为(![]() ,
,![]() ).
).
(3)设yAE=k1x+b1,yAF=k2x+b2,
经过点A(2,0),
∴yAE=k1x﹣2k1,yAF=k2x﹣2k1,
∴OM=2k1,ON=2k2,
∵OMON=2,
∴k1k2=![]() ,
,
直线AE与抛物线的交点为:![]() x2﹣3x+4=k1x﹣2k1,
x2﹣3x+4=k1x﹣2k1,
∴E(4+2k1,2k12+2k1),F(4+2k2,2k22+2k2),
∴EF所在直线解析式为:y=(k1+k2+1)x﹣(4k1+4k2+5),
∴EF直线过定点(4,﹣1),此点到原点的距离为定值,
∴P(4,﹣1);

 阅读快车系列答案
阅读快车系列答案