Question

【题目】综合与实践

问题情境

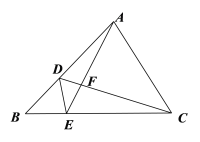
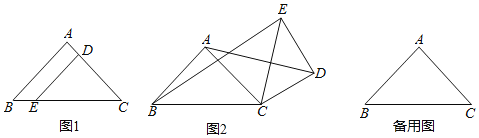
数学课上，李老师提出了这样一个问题：如图1，点是正方形内一点，，，.你能求出的度数吗？

(1)小敏与同桌小聪通过观察、思考、讨论后，得出了如下思路：

思路一：将绕点逆时针旋转，得到，连接，求出的度数.

思路二：将绕点顺时针旋转，得到，连接，求出的度数.

请参考以上思路，任选一种写出完整的解答过程.

类比探究

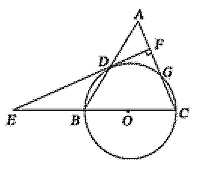
(2)如图2，若点是正方形外一点，，，，求的度数.

拓展应用

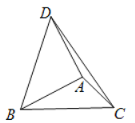
(3)如图3，在边长为的等边三角形内有一点，，，则的面积是______.

Answer 1

【答案】(1)∠APB=135°，(2)∠APB=45°；(3).

【解析】

（1）思路一、先利用旋转求出∠PBP'=90°，BP'=BP=2，AP'=CP=3，利用勾股定理求出PP'，进而判断出△APP'是直角三角形，得出∠APP'=90°，即可得出结论；
思路二、同思路一的方法即可得出结论；

（2）将绕点逆时针旋转，得到，连接，然后同（1）的思路一的方法即可得出结论；

（3）可先将△APB绕点A按逆时针方向旋转60°，得到△AP'C，根据旋转性质，角的计算可得到△APP'是等边三角形，再根据勾股定理，得到AP的长，最后根据三角形面积得到所求．

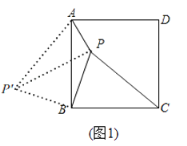
解：(1)思路一，如图1，

将绕点逆时针旋转，得到，连接，

则≌，，

，，

∴，

根据勾股定理得，，

∵，

∴.

又∵，

∴，

∴是直角三角形，且，

∴；

思路二、同思路一的方法.

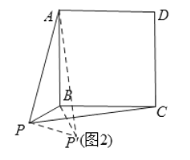
(2)如图2，将绕点逆时针旋转，得到，连接，

则≌，，，，

∴，

根据勾股定理得，.

∵，

∴.

又∵，

∴，

∴是直角三角形，且，

∴；

（3）如图3，将△APB绕点A按逆时针方向旋转60°，得到△AP'C，

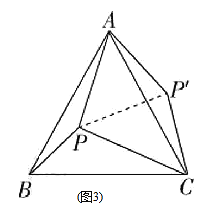
∴∠AP'C＝∠APB＝360°-90°-120°＝150°．

∵AP＝AP'，

∴△APP'是等边三角形，

∴PP'＝AP，∠AP'P＝∠APP'＝60°，

∴∠PP'C＝90°，∠P'PC＝30°，

∴，即．

∵APC＝90°，

∴AP2＋PC2＝AC2，且，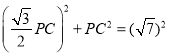

∴PC＝2，

∴，

∴．