Question

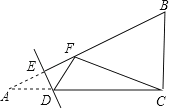
【题目】如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，点E是AB边上一动点，过点E作DE⊥AB交AC边于点D，将∠A沿直线DE翻折，点A落在线段AB上的F处，连接FC，当△BCF为等腰三角形时，AE的长为_____．

Answer 1

【答案】2或或．

【解析】

由勾股定理求出AB，设AE=x，则EF=x，BF=10﹣2x；分三种情况讨论：

①当BF=BC时，列出方程，解方程即可；

②当BF=CF时，F在BC的垂直平分线上，得出AF=BF，列出方程，解方程即可；

③当CF=BC时，作CG⊥AB于G，则BG=FGBF，由射影定理求出BG，再解方程即可．

由翻折变换的性质得：AE=EF．

∵∠ACB=90°，AC=8，BC=6，

∴AB10．

设AE=x，则EF=x，BF=10﹣2x．

分三种情况讨论：

①当BF=BC时，10﹣2x=6，

解得：x=2，

∴AE=2；

②当BF=CF时．

∵BF=CF，

∴∠B=∠FCB．

∵∠A+∠B=90°，∠FCA+∠FCB=90°，

∴∠A=∠FCA，

∴AF= FC．

∵BF=FC，

∴AF=BF，

∴x+x=10﹣2x，

解得：x，

∴AE；

③当CF=BC时，作CG⊥AB于G，如图所示：

则BG=FGBF．

根据射影定理得：BC2=BGAB，

∴BG，

即(10﹣2x)，

解得：x，

∴AE；

综上所述：当△BCF为等腰三角形时，AE的长为：2或或．

故答案为：2或或．