题目内容
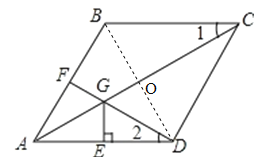
【题目】已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论中一定成立的是_____(把所有正确结论的序号都填在横线上).①DF⊥AB;②CG=2GA;③CG=DF+GE;④S四边形BFGC=![]() ﹣1.
﹣1.
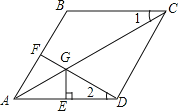
【答案】①②③
【解析】
①由四边形ABCD是菱形,得出对角线平分对角,求得∠GAD=∠2,得出AG=GD,AE=ED,由SAS证得△AFG≌△AEG,得出∠AFG=∠AEG=90°,即可得出①正确;
②由DF⊥AB,F为边AB的中点,证得AD=BD,证出△ABD为等边三角形,得出∠BAC=∠1=∠2=30°,由AC=2ABcos∠BAC,AG![]() ,求出AC,AG,即可得出②正确;
,求出AC,AG,即可得出②正确;
③由勾股定理求出DF![]() ,由GE=tan∠2ED求出GE,即可得出③正确;
,由GE=tan∠2ED求出GE,即可得出③正确;
④由S四边形BFGC=S△ABC﹣S△AGF求出数值,即可得出④不正确.
∵四边形ABCD是菱形,
∴∠FAG=∠EAG,AB=AD,BC∥AD,
∴∠1=∠GAD.
∵∠1=∠2,
∴∠GAD=∠2,
∴AG=GD.
∵GE⊥AD,
∴GE垂直平分AD,
∴AE=ED.
∵F为边AB的中点,
∴AF=AE,
在△AFG和△AEG中,
∵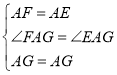 ,
,
∴△AFG≌△AEG(SAS),
∴∠AFG=∠AEG=90°,
∴DF⊥AB,
∴①正确;
连接BD交AC于点O.
∵DF⊥AB,F为边AB的中点,
∴AF![]() AB=1,AD=BD.
AB=1,AD=BD.
∵AB=AD,
∴AD=BD=AB,
∴△ABD为等边三角形,
∴∠BAD=∠BCD=60°,
∴∠BAC=∠1=∠2=30°,
∴AC=2AO=2ABcos∠BAC=2×2![]() 2
2![]() ,
,
AG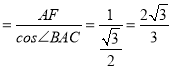 ,
,
∴CG=AC﹣AG=2![]() ,
,
∴CG=2GA,
∴②正确;
∵GE垂直平分AD,
∴ED![]() AD=1,
AD=1,
由勾股定理得:DF![]() ,
,
GE=tan∠2ED=tan30°×1![]() ,
,
∴DF+GE![]() span>CG,
span>CG,
∴③正确;
∵∠BAC=∠1=30°,
∴△ABC的边AC上的高等于AB的一半,即为1,
FG![]() AG
AG![]() ,
,
S四边形BFGC=S△ABC﹣S△AGF![]() 2
2![]() 1
1![]() 1
1![]() ,
,
∴④不正确.
故答案为:①②③.