题目内容
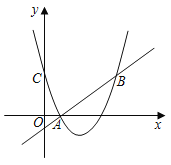
【题目】对于平面直角坐标系![]() 中,已知点A(-2,0)和点B(3,0),线段AB和线段AB外的一点P,给出如下定义:若45°≤∠APB≤90°时,则称点P为线段AB的可视点,且当PA=PB时,称点P为线段AB的正可视点.
中,已知点A(-2,0)和点B(3,0),线段AB和线段AB外的一点P,给出如下定义:若45°≤∠APB≤90°时,则称点P为线段AB的可视点,且当PA=PB时,称点P为线段AB的正可视点.
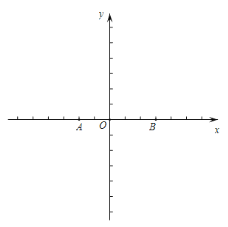
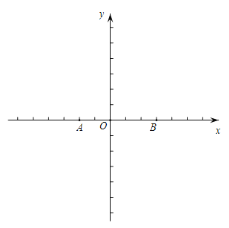
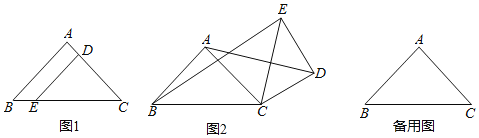
图1 备用图
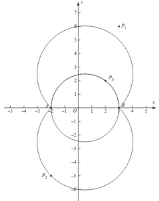
(1) ①如图1,在点P1(3,6),P2(-2,-5),P3(2,2)中,线段AB的可视点是 ;
②若点P在y轴正半轴上,写出一个满足条件的点P的坐标:__________.
(2)在直线y=x+b上存在线段AB的可视点,求b的取值范围;
(3)在直线y=-x+m上存在线段AB的正可视点,直接写出m的取值范围.
【答案】(1)①线段AB的可视点是![]() ,
,![]() ; ②点P的坐标:P(0,3)(答案不唯一,纵坐标
; ②点P的坐标:P(0,3)(答案不唯一,纵坐标![]() 范围:
范围:![]() ≤
≤![]() ≤6);(2)b的取值范围是:-8≤b≤7; (3)m的取值范围:
≤6);(2)b的取值范围是:-8≤b≤7; (3)m的取值范围:![]() 或
或![]()
【解析】
(1)根据题意画出图形,进一步即可得出结论;
(2)正确画出相关图形进一步证明即可;
(3)根据题意,正确画出图形,根据相关量之间的关系进一步求解即可.
(1)①线段AB的可视点是![]() ,
,![]() .
.
②点P的坐标:P(0,3)(答案不唯一,纵坐标![]() 范围:
范围:![]() ≤
≤![]() ≤6).
≤6).
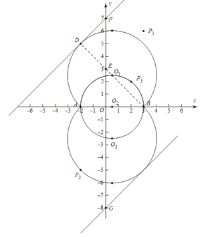
(2)如图,直线与⊙![]() 相切时,BD是⊙
相切时,BD是⊙![]() 直径
直径
∴BD=![]() .
.
∵BE=![]() ,
,
∴DE=![]() .
.
∴EF=![]() =4.
=4.
∴F(0,7)
同理可得,
直线与⊙![]() 相切时,G(0,-8)
相切时,G(0,-8)
∴b的取值范围是:-8≤b≤7.
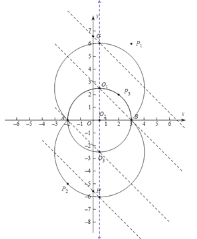
(3)m的取值范围:![]() 或
或![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
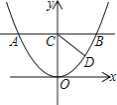
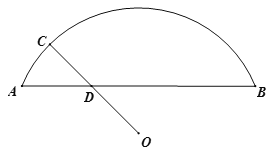
小学生10分钟应用题系列答案【题目】如图,O是![]() 所在圆的圆心,C是
所在圆的圆心,C是![]() 上一动点,连接OC交弦AB于点D.已知AB=9.35cm,设A,D两点间的距离为
上一动点,连接OC交弦AB于点D.已知AB=9.35cm,设A,D两点间的距离为![]() cm,O,D两点间的距离为
cm,O,D两点间的距离为![]() cm,C,D两点间的距离为
cm,C,D两点间的距离为![]() cm.小腾根据学习函数的经验,分别对函数
cm.小腾根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.下面是小腾的探究过程,请补充完整:
的变化而变化的规律进行了探究.下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量![]() 的值进行取点、画图、测量,分别得到了
的值进行取点、画图、测量,分别得到了![]() ,
,![]() 与
与![]() 的几组对应值:
的几组对应值:
| 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 | 7.10 | 8.00 | 9.35 |
| 4.93 | 3.99 |
| 2.28 | 1.70 | 1.59 | 2.04 | 2.88 | 3.67 | 4.93 |
| 0.00 | 0.94 | 1.83 | 2.65 | 3.23 | 3.34 | 2.89 | 2.05 | 1.26 | 0.00 |
(2)①在同一平面直角坐标系![]() 中,描出表中各组数值所对应的点(
中,描出表中各组数值所对应的点(![]() ,
,![]() ), (
), (![]() ,
,![]() ),并画出(1)中所确定的函数
),并画出(1)中所确定的函数![]() ,
,![]() 的图象;
的图象;
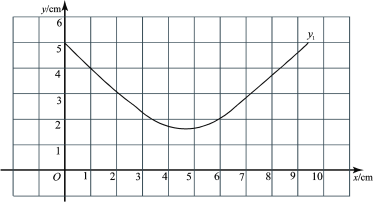
②观察函数![]() 的图象,可得
的图象,可得![]() cm(结果保留一位小数);
cm(结果保留一位小数);
(