题目内容
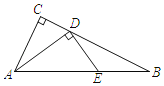
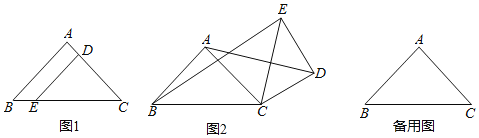
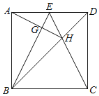
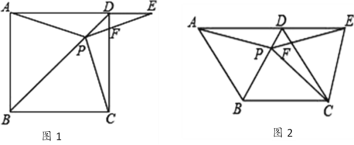
【题目】如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:△APD≌△CPD;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
【答案】(1)证明见解析;(2)90°;(3)AP=CE.
【解析】
(1)利用正方形得到AD=CD,∠ADP=∠CDP=45![]() ,即可证明全等;
,即可证明全等;
(2)设![]() ,利用三角形内角和性质及外角性质得到
,利用三角形内角和性质及外角性质得到![]() ,
,![]() ,再利用周角计算得出x值;
,再利用周角计算得出x值;
(3)AP=CE. 设![]() ,利用三角形内角和性质及外角性质得到
,利用三角形内角和性质及外角性质得到![]() ,
,
![]() ,求出
,求出![]() ,得到
,得到![]() 是等边三角形,即可证得AP=CE.
是等边三角形,即可证得AP=CE.
解:
(1)![]() 四边形ABCD是正方形,
四边形ABCD是正方形,
∴AD=CD,∠ADP=∠CDP=45![]() ,
,
在![]() 与
与![]() 中,
中,
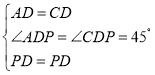 ,
,
∴![]() ;
;
(2)设![]() ,
,
由(1)得,![]() ,
,![]()
因为PA=PE,所以![]()
所以![]() ;
;
(3)AP=CE.
设![]() ,
,
由(1)得,![]() ,
,![]()
∵PA=PE且在菱形ABCD中![]() ,
,
∴![]() ,
,
∴![]() ,
,
由(1)得PA=PC,∴PC=PE,
∴![]() 是等边三角形,
是等边三角形,
∴PE=PC=CE,
∴AP=CE.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
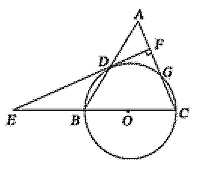
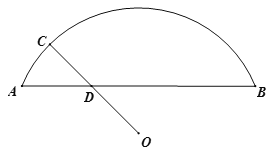
小学生10分钟应用题系列答案【题目】如图,O是![]() 所在圆的圆心,C是
所在圆的圆心,C是![]() 上一动点,连接OC交弦AB于点D.已知AB=9.35cm,设A,D两点间的距离为
上一动点,连接OC交弦AB于点D.已知AB=9.35cm,设A,D两点间的距离为![]() cm,O,D两点间的距离为
cm,O,D两点间的距离为![]() cm,C,D两点间的距离为
cm,C,D两点间的距离为![]() cm.小腾根据学习函数的经验,分别对函数
cm.小腾根据学习函数的经验,分别对函数![]() ,
,![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.下面是小腾的探究过程,请补充完整:
的变化而变化的规律进行了探究.下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量![]() 的值进行取点、画图、测量,分别得到了
的值进行取点、画图、测量,分别得到了![]() ,
,![]() 与
与![]() 的几组对应值:
的几组对应值:
| 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 | 7.10 | 8.00 | 9.35 |
| 4.93 | 3.99 |
| 2.28 | 1.70 | 1.59 | 2.04 | 2.88 | 3.67 | 4.93 |
| 0.00 | 0.94 | 1.83 | 2.65 | 3.23 | 3.34 | 2.89 | 2.05 | 1.26 | 0.00 |
(2)①在同一平面直角坐标系![]() 中,描出表中各组数值所对应的点(
中,描出表中各组数值所对应的点(![]() ,
,![]() ), (
), (![]() ,
,![]() ),并画出(1)中所确定的函数
),并画出(1)中所确定的函数![]() ,
,![]() 的图象;
的图象;
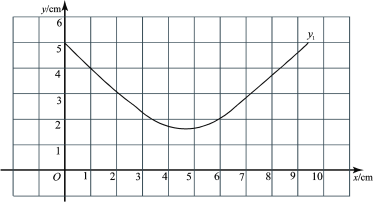
②观察函数![]() 的图象,可得
的图象,可得![]() cm(结果保留一位小数);
cm(结果保留一位小数);
(