题目内容
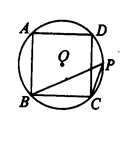
如图,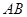 是
是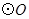 的直径,弦
的直径,弦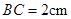 ,
,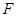 是弦
是弦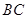 的中点,
的中点,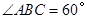 .若动点
.若动点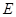 以
以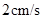 的速度从
的速度从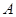 点出发沿着
点出发沿着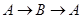 方向运动,设运动时间为
方向运动,设运动时间为 ,连结
,连结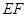 ,当
,当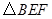 是直角三角形时,
是直角三角形时,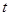 (s)的值为
(s)的值为
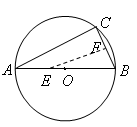
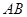 是
是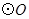 的直径,弦
的直径,弦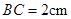 ,
,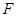 是弦
是弦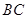 的中点,
的中点,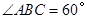 .若动点
.若动点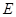 以
以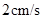 的速度从
的速度从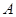 点出发沿着
点出发沿着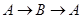 方向运动,设运动时间为
方向运动,设运动时间为 ,连结
,连结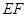 ,当
,当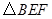 是直角三角形时,
是直角三角形时,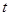 (s)的值为
(s)的值为
A.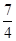 | B.1 | C.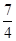 或1 或1 | D.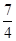 或1 或 或1 或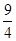 |
D
析:若△BEF是直角三角形,则有两种情况:①∠BFE=90°,②∠BEF=90°;在上述两种情况所得到的直角三角形中,已知了BC边和∠B的度数,即可求得BE的长;AB的长易求得,由AE=AB-BE即可求出AE的长,也就能得出E点运动的距离,根据时间=路程÷速度即可求得t的值.
解答:解:∵AB是⊙O的直径,
∴∠ACB=90°;
Rt△ABC中,BC=2,∠ABC=60°;
∴AB=2BC=4cm;
①当∠BFE=90°时;
Rt△BEF中,∠ABC=60°,则BE=2BF=2cm;
故此时AE=AB-BE=2cm;
∴E点运动的距离为:2cm,故t=1s;
所以当∠BFE=90°时,t=1s;
②当∠BEF=90°时;
同①可求得BE=0.5cm,此时AE=AB-BE=3.5cm;
∴E点运动的距离为:3.5cm,故t=1.75s;
③当E从B回到O的过程中,在运动的距离是:2(4-3.5)=1cm,则时间是:1.75+ =
= s.
s.
综上所述,当t的值为1s或1.75s和 s时,△BEF是直角三角形.
s时,△BEF是直角三角形.
故选D.
解答:解:∵AB是⊙O的直径,
∴∠ACB=90°;

Rt△ABC中,BC=2,∠ABC=60°;
∴AB=2BC=4cm;
①当∠BFE=90°时;
Rt△BEF中,∠ABC=60°,则BE=2BF=2cm;
故此时AE=AB-BE=2cm;
∴E点运动的距离为:2cm,故t=1s;
所以当∠BFE=90°时,t=1s;
②当∠BEF=90°时;
同①可求得BE=0.5cm,此时AE=AB-BE=3.5cm;
∴E点运动的距离为:3.5cm,故t=1.75s;
③当E从B回到O的过程中,在运动的距离是:2(4-3.5)=1cm,则时间是:1.75+
 =
= s.
s.综上所述,当t的值为1s或1.75s和
 s时,△BEF是直角三角形.
s时,△BEF是直角三角形.故选D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ABC的两直角边AC、BC分别是一元二次方程
ABC的两直角边AC、BC分别是一元二次方程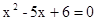 的两根,则此Rt
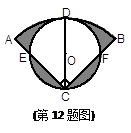
的两根,则此Rt 图2是某巷子的俯视图,巷子路面宽4 m,转弯处为直角,车辆的车身为矩形ABCD,CD与DE、CE的夹角都是45°时,连
图2是某巷子的俯视图,巷子路面宽4 m,转弯处为直角,车辆的车身为矩形ABCD,CD与DE、CE的夹角都是45°时,连 接EF,交CD于点G,若GF的长度至少能达到车身宽度,即车辆能通过.
接EF,交CD于点G,若GF的长度至少能达到车身宽度,即车辆能通过. 为半径的弧),长8m,宽3m的消防车就可以通过该弯道了,具体的方案如图3,其中OM⊥OM′,你能帮小平算出,ON至少为多少时,这种消防车可以通过该巷子,?
为半径的弧),长8m,宽3m的消防车就可以通过该弯道了,具体的方案如图3,其中OM⊥OM′,你能帮小平算出,ON至少为多少时,这种消防车可以通过该巷子,?
 与
与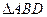 的边
的边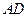 相切于点
相切于点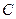 ,
,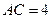 ,
,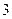 ,当
,当 与
与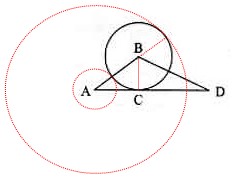
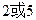
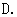
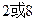


 ,
, ,则向量
,则向量 可表示为( ).
可表示为( ).




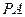 为
为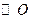 的切线,
的切线,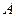 为切点,
为切点,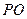 交
交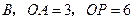 ,求
,求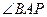 的度数.
的度数.