题目内容
已知Rt ABC的两直角边AC、BC分别是一元二次方程
ABC的两直角边AC、BC分别是一元二次方程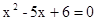 的两根,则此Rt
的两根,则此Rt 的外接圆的面积为 。
的外接圆的面积为 。
 ABC的两直角边AC、BC分别是一元二次方程
ABC的两直角边AC、BC分别是一元二次方程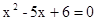 的两根,则此Rt
的两根,则此Rt 的外接圆的面积为 。
的外接圆的面积为 。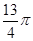 。
。首先解出一元二次方程的两根,再利用直角三角形的外接圆半径与斜边的关系可以解决.
解:解方程x2-5x+6=0,
得:x1=2,x2=3,
即两直角边AC、BC是2或3,
根据勾股定理得:
斜边长为: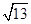 ,
,
也就是Rt△ABC的外接圆直径为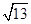 ,
,
∴Rt△ABC的外接圆的面积为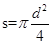 =
=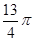 .
.
故填: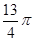 .
.
解:解方程x2-5x+6=0,
得:x1=2,x2=3,
即两直角边AC、BC是2或3,
根据勾股定理得:
斜边长为:
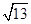 ,
,也就是Rt△ABC的外接圆直径为
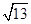 ,
,∴Rt△ABC的外接圆的面积为
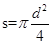 =
=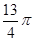 .
.故填:
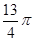 .
.
练习册系列答案
相关题目
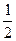 ,OD=20.
,OD=20.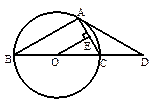
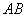 为半圆
为半圆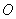 的直径,延长
的直径,延长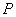 ,使
,使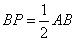 ,
,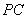 切半圆
切半圆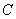 ,点
,点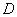 是弧AC上和点
是弧AC上和点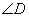 的度数为 .(圆的性质、切线的性质、解三角形)
的度数为 .(圆的性质、切线的性质、解三角形) 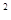 。(不考虑接缝等因素,计算结果用
。(不考虑接缝等因素,计算结果用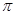 表示)
表示)
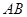 是
是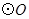 的直径,弦
的直径,弦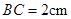 ,
,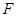 是弦
是弦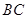 的中点,
的中点,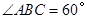 .若动点
.若动点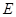 以
以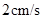 的速度从
的速度从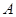 点出发沿着
点出发沿着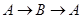 方向运动,设运动时间为
方向运动,设运动时间为 ,连结
,连结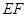 ,当
,当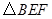 是直角三角形时,
是直角三角形时,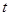 (s)的值为
(s)的值为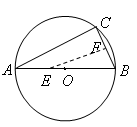
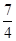
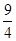
 ∠B=53°.点O为BC边上的一个点,连结OD,以O为圆心,BO为半径的⊙O分别交边AB于点P,交线段OD于点M,交射线BC于点N,连结MN.
∠B=53°.点O为BC边上的一个点,连结OD,以O为圆心,BO为半径的⊙O分别交边AB于点P,交线段OD于点M,交射线BC于点N,连结MN.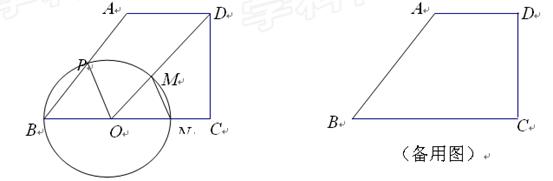
 过程中,线段 BP与MN能否相等?若能,请求出当BO为多长时BP=MN;若不能,请说明理由;
过程中,线段 BP与MN能否相等?若能,请求出当BO为多长时BP=MN;若不能,请说明理由; 3°≈0.6;sin53°≈0.8;t
3°≈0.6;sin53°≈0.8;t an74°
an74° 3.5)
3.5)