题目内容
如图所示,在直角坐标系xOy中,A,B是x轴上两点,以AB为直径的圆交y轴于点C,设过A、B、C三点的抛物线关系为 y=x2-mx+n,若方程x2-mx+n=0两根倒数和为-2.
y=x2-mx+n,若方程x2-mx+n=0两根倒数和为-2.
(1)求n的值;
(2)求此抛物线的关系式.
 y=x2-mx+n,若方程x2-mx+n=0两根倒数和为-2.
y=x2-mx+n,若方程x2-mx+n=0两根倒数和为-2.(1)求n的值;
(2)求此抛物线的关系式.
(1)由题意,设A(x1,0),B(x2,0),C(0,n)
∵OA=-x1,OB=x2,又CO⊥AB,
∴CO2=AO•OB,
即n2=-x1x2;
又∵x1,x2是方程x2-mx+n=0的两根,
∴x1•x2=n,
∴n2=-n,
∴n1=-1,n2=0(舍去),
∴n=-1.
(2)∵x1,x2是方程x2-mx+n=0的两根,
∴x1+x2=m.
又∵n=-1,
∴x1x2=-1,
∴
+
=
=
=-2,
∴m=2,
∴所求抛物线的关系式为y=x2-2x-1.
∵OA=-x1,OB=x2,又CO⊥AB,
∴CO2=AO•OB,
即n2=-x1x2;
又∵x1,x2是方程x2-mx+n=0的两根,
∴x1•x2=n,
∴n2=-n,
∴n1=-1,n2=0(舍去),
∴n=-1.
(2)∵x1,x2是方程x2-mx+n=0的两根,
∴x1+x2=m.
又∵n=-1,
∴x1x2=-1,
∴
| 1 |
| x1 |
| 1 |
| x2 |
| x1+x2 |
| x1x2 |
| m |
| -1 |
∴m=2,
∴所求抛物线的关系式为y=x2-2x-1.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
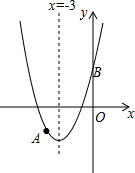
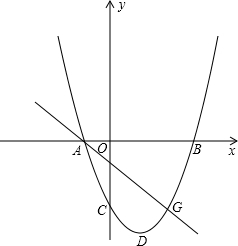 x轴交于A、B两点,其中B点的坐标为(3,0),且OB=OC.
x轴交于A、B两点,其中B点的坐标为(3,0),且OB=OC.


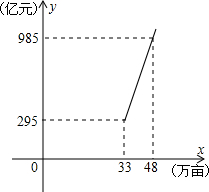 用地总量x(万亩)之间存在着如图所示的一次函数关系.
用地总量x(万亩)之间存在着如图所示的一次函数关系.