题目内容
【题目】如图,已知BC=DE,∠BCF=∠EDF,AF垂直平分CD.求证:∠B=∠E. 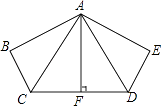
【答案】证明: ∵AF垂直平分CD,
∴AC=AD,∠ACD=∠ADC,
∵∠BCF=∠EDF,
∵∠BCF﹣∠ACD=∠EDF﹣∠ADC,
∴∠BCA=∠EDA,
在△ABC和△AED中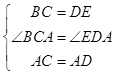 ,
,
∴△ABC≌△AED(SAS),
∴∠B=∠E.
【解析】由已知条件和垂直平分线的性质易证∠BCA=∠EDA,再结合全等三角形的判断方法即可证明△ABC≌△AED,由全等三角形的性质:对应角相等即可得到∠B=∠E.
【考点精析】利用线段垂直平分线的性质对题目进行判断即可得到答案,需要熟知垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目