Question

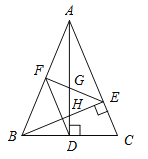
【题目】如图，在△ABC中，AD和BE是高，∠ABE=45°，点F是AB的中点，AD与FE、BE分别交于点G、H，∠CBE=∠BAD．有下列结论：①FD=FE；②AH=2CD；③BCAD=；④S△ABC=4S△ADF．其中正确的有（ ）

A．1个 B．2 个 C．3 个 D．4个

Answer 1

【答案】D．

【解析】

试题分析：∵在△ABC中，AD和BE是高，∴∠ADB=∠AEB=∠CEB=90°，∵点F是AB的中点，∴FD=AB，∵∠ABE=45°，∴△ABE是等腰直角三角形，∴AE=BE，∵点F是AB的中点，∴FE=AB，∴FD=FE，①正确；

∵∠CBE=∠BAD，∠CBE+∠C=90°，∠BAD+∠ABC=90°，∴∠ABC=∠C，∴AB=AC，∵AD⊥BC，∴BC=2CD，∠BAD=∠CAD=∠CBE，在△AEH和△BEC中，∵∠AEH=∠CEB，AE=BE，∠EAH=∠CBE，∴△AEH≌△BEC（ASA），∴AH=BC=2CD，②正确；

∵∠BAD=∠CBE，∠ADB=∠CEB，∴△ABD～△BCE，∴，即BCAD=ABBE，∵=ABAE=ABBE，BCAD=ACBE=ABBE，∴BCAD=；③正确；

∵F是AB的中点，BD=CD，∴S△ABC=2S△ABD=4S△ADF．④正确；

故选D．